
题目列表(包括答案和解析)
 23、2006年“五•一”黄金周心连心集团湖南岳阳超市,七天销售总额达120万元,具体分配情况如图.
23、2006年“五•一”黄金周心连心集团湖南岳阳超市,七天销售总额达120万元,具体分配情况如图.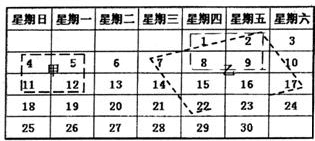
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
 =3.
=3.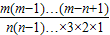
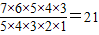 种不同的选法.
种不同的选法. ;水平地面上重1500N的物体,与地面的接触面积为xm2,那么该物体对地面压强y(N/m2)可以表示为,
;水平地面上重1500N的物体,与地面的接触面积为xm2,那么该物体对地面压强y(N/m2)可以表示为,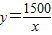 ;函数关系式
;函数关系式 还可以表示许多不同情境中变量之间的关系,请你再列举1例: .
还可以表示许多不同情境中变量之间的关系,请你再列举1例: .湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com