20080924
三、解答题：（本大题共6小题，共74分）
17．解：（Ⅰ）∵
∴函数
的最小正周期
（Ⅱ）∵
， ∴
∴
∴
∴函数
时的值域为[－1，2]
18．解：（Ⅰ）记“任取2个乒乓球，恰好取得1个黄色乒乓球”为事件A，则
（Ⅱ）记“第一次取得白色乒乓球时，恰好已取出1个黄色乒乓球”为事件B；记“第一次取得白色乒乓球时，恰好已取出2个黄色乒乓球”为事件C. 则
∵事件B与事件C是互斥事件，
∴第一次取得白色乒乓球时，已取出的黄色乒乓球个数不少于1个的概率为
P（B+C）=P（B）+P（C）=
19．解：（1）∵SD⊥AD，SD⊥AB，AD∩AB=A∴SD⊥平面ABCD，
又∵SD
平面SBD， ∴平面SDB⊥平面ABCD。
（2）由（1）知平面SDB⊥平面ABCD，
BD为平面SDB与平面ABCD的交线，过点A作AE⊥DB于E，则AE⊥平面SDB，
由三垂线定理的逆定理得 EF⊥SB， ∴∠AFE为二面角A―SB―D的平面角。 在矩形ABCD中，设AD=a，则 ， 在Rt△SBC中， 而在Rt△SAD中，SA=2a，又AB=2a，∴SB2=SA2+AB2， 即△SAB为等腰直角三角形，且∠SAB为直角， ∴ ∴ 故二面角A―SB―D的大小为  20．解：（Ⅰ）设等差数列{an}的公差为d，由题意 
∴ （Ⅱ）∵ ∴ ∴数列{bn}的前n项和 
 21．解：（Ⅰ）由题，得 ，设 则 由 …………① 又 在双曲线上，则 …………② 联立①、②，解得  由题意，  ∴点T的坐标为（2，0） （Ⅱ）设直线A1P与直线A2Q的交点M的坐标为（x，y） 由A1、P、M三点共线，得  …………③
由A2、Q、M三点共线，得  …………④
联立③、④，解得  ∵在双曲线上， ∴ ∴轨迹E的方程为 22．解：（Ⅰ）设P（x，y）是函数 图象上的任意一点，它在函数 图象上的对应点 ，则由平移公式，得 ∴ 代入函数 中，得  ∴函数的表达式为 （Ⅱ）函数 的对称轴为 ①当 时，函数在[ ]上为增函数， ∴ ②当 时， ∵ 令 ∴ ③当 时，函数在[]上为减函数， ∴ 而 ，应舍去 综上所述，有
| |
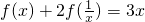，求f（x）的表达式．
，求f（x）的表达式．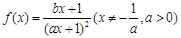
，且
，
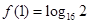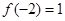
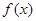的表达式；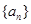
的项满足
，试求
，
，
，
；
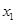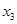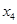的通项；