
题目列表(包括答案和解析)
材料:采访零向量
W:你好!零向量.我是《数学天地》的一名记者,为了让在校的高中生更好了解你,能不能对你进行一次采访呢?
零向量:当然可以,我们向量王国随时恭候大家的光临,很乐意接受你的采访,让高中生朋友更加了解我,更好地为他们服务.
W:好的,那就开始吧!你的名字有什么特殊的含义吗?
零向量:零向量就是长度为零的向量,它与数字0有着密切的联系,所以用0来表示我.
W:你与其他向量有什么共同之处呢?
零向量:既然我是向量王国的一个成员,就具有向量的基本性质,如既有大小又有方向,在进行加、减法运算时满足交换律和结合律,还定义了与实数的积.
W:你有哪些值得骄傲的特殊荣耀呢?
零向量:首先,我的方向是不定的,可以与任意的向量平行.其次,我还有其他一些向量所没有的特殊待遇:如我的相反向量仍是零向量;在向量的线性运算中,我与实数0很有相似之处.
W:你有如此多的荣耀,那么是否还有烦恼之事呢?
零向量:当然有了,在向量王国还有许多“权利和义务”却大有把我排斥在外之意,如平行向量的定义,向量共线定理,两向量夹角的定义都对我进行了限制.所有这些确实给一些高中生带来了很多苦恼,在此我向大家真诚地说一声:对不起,这不是我的错.但我还是很高兴有这次机会与大家见面.
W:OK!采访就到这里吧,非常感谢你的合作,再见!
零向量:Bye!
阅读上面的材料回答下面问题.
应用零向量时应注意哪些问题?
蜜蜂蜂房是严格的六角柱状体,它的一端是平整的六角形开口,另一端是封闭的六角菱锥形的底,由三个相同的菱形组成.组成底盘的菱形的钝角为109度28分,所有的锐角为70度32分,这样既坚固又省料.蜂房的巢壁厚0.073毫米,误差极小.
丹顶鹤总是成群结队迁飞,而且排成“人”字形.“人”字形的角度是110度.更精确地计算还表明“人”字形夹角的一半——即每边与鹤群前进方向的夹角为54度44分8秒!而金刚石结晶体的角度正好也是54度44分8秒!是巧合还是某种大自然的“默契”?
蜘蛛结的“八卦”形网,是既复杂又美丽的八角形几何图案,人们即使用直尺的圆规也很难画出像蜘蛛网那样匀称的图案.
冬天,猫睡觉时总是把身体抱成一个球形,这其间也有数学,因为球形使身体的表面积最小,从而散发的热量也最少.
真正的数学“天才”是珊瑚虫.珊瑚虫在自己的身上记下“日历”,它们每年在自己的体壁上“刻画”出365条斑纹,显然是一天“画”一条.奇怪的是,古生物学家发现3亿5千万年前的珊瑚虫每年“画”出400幅“水彩画”.天文学家告诉我们,当时地球一天仅21.9小时,一年不是365天,而是400天.
1.同学们,大自然中有许多有关数学的奥妙,许多现象有意无意地应用着数学,对于这些现象你有什么看法吗?请你谈谈你对大自然中的数学现象的认识.
2.把你发现的大自然中的数学问题告诉你的同学和老师,让他们也分享一下你认识大自然的乐趣.
如图所示的长方体 中,底面
中,底面 是边长为
是边长为 的正方形,
的正方形, 为
为 与
与 的交点,
的交点, ,
, 是线段
是线段 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求二面角 的大小.
的大小.
【解析】本试题主要考查了线面平行的判定定理和线面垂直的判定定理,以及二面角的求解的运用。中利用 ,又
,又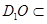 平面
平面 ,
, 平面
平面 ,∴
,∴ 平面
平面 由
由 ,
, ,又
,又 ,∴
,∴ 平面
平面 .
可得证明
.
可得证明
(3)因为∴ 为面
为面 的法向量.∵
的法向量.∵ ,
, ,
,
∴ 为平面
为平面 的法向量.∴利用法向量的夹角公式,
的法向量.∴利用法向量的夹角公式, ,
,
∴ 与
与 的夹角为
的夹角为 ,即二面角
,即二面角 的大小为
的大小为 .
.
方法一:解:(Ⅰ)建立如图所示的空间直角坐标系.连接 ,则点
,则点 、
、 ,
,

∴ ,又点
,又点 ,
, ,∴
,∴
∴ ,且
,且 与
与 不共线,∴
不共线,∴ .
.
又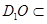 平面
平面 ,
, 平面
平面 ,∴
,∴ 平面
平面 .…………………4分
.…………………4分
(Ⅱ)∵ ,
,
∴ ,
, ,即
,即 ,
, ,
,
又 ,∴
,∴ 平面
平面 . ………8分
. ………8分
(Ⅲ)∵ ,
, ,∴
,∴ 平面
平面 ,
,
∴ 为面
为面 的法向量.∵
的法向量.∵ ,
, ,
,
∴ 为平面
为平面 的法向量.∴
的法向量.∴ ,
,
∴ 与
与 的夹角为
的夹角为 ,即二面角
,即二面角 的大小为
的大小为
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1.
(Ⅰ)证明PC⊥AD;
(Ⅱ)求二面角A-PC-D的正弦值;
(Ⅲ)设E为棱PA上的点,满足异面直线BE与CD所成的角为30°,求AE的长.

【解析】解法一:如图,以点A为原点建立空间直角坐标系,依题意得A(0,0,0),D(2,0,0),C(0,1,0), 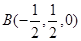 ,P(0,0,2).
,P(0,0,2).

(1)证明:易得 ,
, 于是
于是 ,所以
,所以
(2)  ,
, 设平面PCD的法向量
设平面PCD的法向量 ,
,
则 ,即
,即 .不防设
.不防设 ,可得
,可得 .可取平面PAC的法向量
.可取平面PAC的法向量 于是
于是 从而
从而 .
.
所以二面角A-PC-D的正弦值为 .
.
(3)设点E的坐标为(0,0,h),其中 ,由此得
,由此得 .
.
由 ,故
,故
所以, ,解得
,解得 ,即
,即 .
.
解法二:(1)证明:由 ,可得
,可得 ,又由
,又由 ,
, ,故
,故 .又
.又 ,所以
,所以 .
.

(2)如图,作 于点H,连接DH.由
于点H,连接DH.由 ,
, ,可得
,可得 .
.
因此 ,从而
,从而 为二面角A-PC-D的平面角.在
为二面角A-PC-D的平面角.在 中,
中, ,由此得
,由此得 由(1)知
由(1)知 ,故在
,故在 中,
中,
因此 所以二面角
所以二面角 的正弦值为
的正弦值为 .
.
(3)如图,因为 ,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF. 故
,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF. 故 或其补角为异面直线BE与CD所成的角.由于BF∥CD,故
或其补角为异面直线BE与CD所成的角.由于BF∥CD,故 .在
.在 中,
中, 故
故

在 中,由
中,由 ,
, ,
,
可得 .由余弦定理,
.由余弦定理, ,
,
所以 .
.
如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
(1) 求证:A1C⊥平面BCDE;
(2) 若M是A1D的中点,求CM与平面A1BE所成角的大小;
(3) 线段BC上是否存在点P,使平面A1DP与平面A1BE垂直?说明理由
【解析】(1)∵ DE∥BC∴
DE∥BC∴ ∴
∴ ∴
∴ ∴
∴ 又∵
又∵ ∴
∴
(2)如图,以C为坐标原点,建立空间直角坐标系C-xyz,

则

设平面 的法向量为
的法向量为 ,则
,则 ,又
,又 ,
, ,所以
,所以 ,令
,令 ,则
,则 ,所以
,所以 ,
,
设CM与平面 所成角为
所成角为 。因为
。因为 ,
,
所以
所以CM与平面 所成角为
所成角为 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com