
题目列表(包括答案和解析)
| a |
| b |
| ab |
| ab |
| ab |
| p |
| p |
| 1 |
| m |
| 8 |
| m-1 |
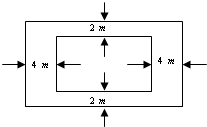
解:因为函数没有零点,所以方程![]() 无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
现有5名同学的物理和数学成绩如下表:
| 物理 | 64 | 61 | 78 | 65 | 71 |
| 数学 | 66 | 63 | 88 | 76 | 73 |
(1)画出散点图;
(2)若![]() 与
与![]() 具有线性相关关系,试求变量
具有线性相关关系,试求变量![]() 对
对![]() 的回归方程并求变量
的回归方程并求变量![]() 对
对![]() 的回归方程.
的回归方程.
(Ⅰ)(20分)在复数范围内解方程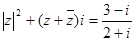 (i为虚数单位)
(i为虚数单位)
(Ⅱ)设z是虚数,ω=z+ 是实数,且-1<ω<2
是实数,且-1<ω<2
(1)求|z|的值及z的实部的取值范围;(10分)
(2)设u=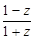 ,求证:u为纯虚数;(5分)
,求证:u为纯虚数;(5分)
(3)求ω-u2的最小值,(5分)
(Ⅰ)(20分)在复数范围内解方程 (i为虚数单位)
(i为虚数单位)
(Ⅱ)设z是虚数,ω=z+ 是实数,且-1<ω<2
是实数,且-1<ω<2
(1)求|z|的值及z的实部的取值范围;(10分)
(2)设u= ,求证:u为纯虚数;(5分)
,求证:u为纯虚数;(5分)
(3)求ω-u2的最小值,(5分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com