
题目列表(包括答案和解析)
给出下列命题:(1)等比数列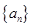 的公比为
的公比为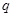 ,则“
,则“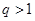 ”是“
”是“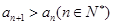 ”的既不充分也不必要条件;(2)“
”的既不充分也不必要条件;(2)“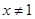 ”是“
”是“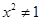 ”的必要不充分条件;(3)函数的
”的必要不充分条件;(3)函数的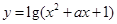 的值域为R,则实数
的值域为R,则实数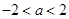 ;(4)“
;(4)“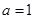 ”是“函数
”是“函数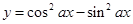 的最小正周期为
的最小正周期为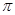 ”的充要条件.其中真命题的个数是
”的充要条件.其中真命题的个数是
A.1 B.2 C.3 D.4
“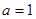 ”是“函数
”是“函数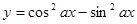 ”的最小正周期为
”的最小正周期为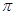 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
“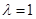 ”是“函数
”是“函数 的最小正周期为
的最小正周期为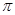 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
下列四个命题中
①“![]() ”是“函数
”是“函数![]() 的最小正周期为
的最小正周期为![]() ”的充要条件;
”的充要条件;
②“![]() ”是“直线
”是“直线![]() 与直线
与直线![]() 相互垂直”的充要条件;
相互垂直”的充要条件;
③ 函数![]() 的最小值为
的最小值为![]()
其中假命题的为 (将你认为是假命题的序号都填上)
以下判断正确的是 ( )
A.命题“负数的平方是正数”不是全称命题
B.命题“ ”的否定是“
”的否定是“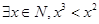 ”
”
C.“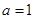 ”是“函数
”是“函数 的最小正周期是
的最小正周期是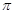 ”的必要不充分条件
”的必要不充分条件
D.“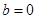 ”是“函数
”是“函数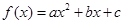 是偶函数”的充要条件
是偶函数”的充要条件
一、选择题
1―5BABAB 6―10DBABA 11―12CC
|