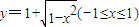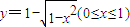20081006 13. 14.
14. 15. 16. f( 16. f( )<f(1)< f( )<f(1)< f( ) ) 三、解答题 17.解:(Ⅰ) , , 
= 是奇函数, 是奇函数, 得 得 , , (Ⅱ)由(Ⅰ)得 , , 从而 在 在 和 和 上增函数, 上增函数, 在 上减函数, 上减函数, 所以 在 在 时取得极大值,极大值为 时取得极大值,极大值为 , , 在 在 时取得极小值,极小值为 时取得极小值,极小值为 18.解:(Ⅰ)设A队得分为2分的事件为 , , 对阵队员  队队员胜 队队员胜
 队队员负 队队员负
 对 对


 对 对


 对 对


 
0 1 2 3 



∴ 的分布列为: 的分布列为:
………… 8分 于是  , …………9分 , …………9分 ∵  , ∴ , ∴
 ………… 11分 ………… 11分 由于 , 故B队比A队实力较强. …………12分 , 故B队比A队实力较强. …………12分 19.解:(1)由 得 得 ∴ ∴ ……………2分 ……………2分 由已知得, ∴ .
从而 .
从而 .……………4分 .……………4分 (2) 由(1)知, , , 即 值域为 值域为 .…………6分 .…………6分 ∴由已知得: 于是……………8分
于是……………8分 
20.解:(Ⅰ) , , 化为 , ,  或 或 解得 或 或 ,原不等式的解集为 ,原不等式的解集为 (Ⅱ) , , ①当 时, 时, 在区间[ 在区间[ ]上单调递增,从而 ]上单调递增,从而 ②当 时,对称轴的方程为 时,对称轴的方程为 ,依题意得 ,依题意得 或 或 解得 解得 或 或 综合①②得 21.解:(Ⅰ) , , 若 =0 得 =0 得 解不等式 ,得 ,得 , , 解不等式 , , 得 得  和 和 , , 从而 的单调递增区间是 的单调递增区间是 ,单调递减区间是 ,单调递减区间是 和 和 (Ⅱ)将 两边取对数得 两边取对数得 , , 因为 ,从而 ,从而 由(Ⅰ)得当 时 时 , , 要使 对任意 对任意 成立,当且仅当 成立,当且仅当 ,得 ,得 22.(Ⅰ)解:  是二次函数,且 是二次函数,且 的解集是 的解集是 , ,  可设 可设 . .
 在区间 在区间 上的最大值是 上的最大值是 . .
由已知,得 . . . .  . .
(Ⅱ)方程 等价于方程 等价于方程 . . 设 , , 则 . . 当 时, 时, 是减函数; 是减函数; 当 时, 时, 是增函数. 是增函数.  , ,
 方程 方程 在区间 在区间 内分别有惟一实数根, 内分别有惟一实数根,
而在区间 内没有实数根. 内没有实数根. 所以存在惟一的自然数 , , 使得方程 在区间 在区间 内有且只有两个不同的实数根. 内有且只有两个不同的实数根. www.ks5u.com
| |

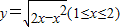 反函数是( )
反函数是( )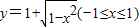
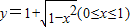
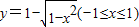

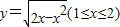 反函数是( )
反函数是( )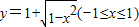

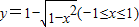
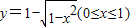
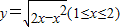 反函数是( )
反函数是( )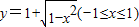
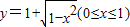
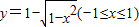
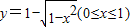
 反函数是( )
反函数是( )



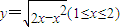 反函数是( )
反函数是( )