
题目列表(包括答案和解析)
| n(n+1) |
| 2 |
| n(n+1)(n+2) |
| 6 |
| 0+2+6 |
| 4 |
| 2(1+3) |
| 4 |
| 0+3+9+18 |
| 9 |
| 3(1+3+6) |
| 9 |
| 10 |
| 3 |
| an |
| an+1 |
| an+1 |
| an |
设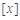 表示不超过
表示不超过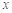 的最大整数,如
的最大整数,如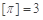 ,
,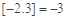 .给出下列命题:
.给出下列命题:
①对任意实数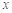 ,都有
,都有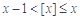 ;
;
②对任意实数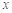 、
、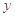 ,都有
,都有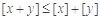 ;③
;③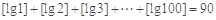 ;
;
④若函数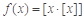 ,当
,当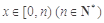 时,令
时,令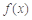 的值域为A,记集合A的元素个数为
的值域为A,记集合A的元素个数为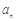 ,则
,则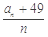 的最小值为
的最小值为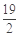 .
.
其中所有真命题的序号是_________________.
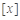 表示不超过
表示不超过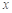 的最大整数,如
的最大整数,如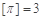 ,
,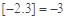 .给出下列命题:
.给出下列命题: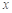 ,都有
,都有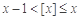 ;
;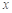 、
、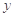 ,都有
,都有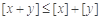 ;③
;③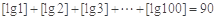 ;
;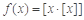 ,当
,当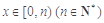 时,令
时,令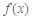 的值域为A,记集合A的元素个数为
的值域为A,记集合A的元素个数为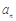 ,则
,则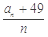 的最小值为
的最小值为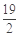 .
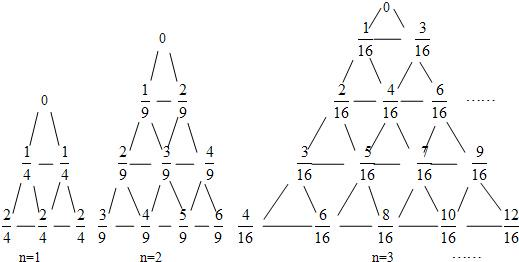
. 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行,从左向右数第
行,从左向右数第 个数。
个数。 
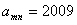 ,求m,n的值;
,求m,n的值; 的反函数为
的反函数为 ,若记三角形数表中从上往下数第n行各数的和为
,若记三角形数表中从上往下数第n行各数的和为 。
。  的前n项的和
的前n项的和 。
。 ,设
,设 的前n项之积为
的前n项之积为 ,求证:
,求证: 。
。 “剪刀、石头、布”游戏的规则是:出拳之前双方齐喊口令,然后在话音刚落时同时出拳,握紧的拳头代表“石头”,食指和中指伸出代表“剪刀”,五指伸开代表“布”.“石头”胜“剪刀”,“剪刀”胜“布”,而“布”又胜“石头”,如果所出的拳相同,则为和局.现甲乙二人通过“剪刀、石头、布”游戏进行比赛.
(Ⅰ)设甲乙二人每局都随机出“剪刀”、“石头”、“布”中的某一个,求甲胜乙的概率;
(Ⅱ)据专家分析,乙有以下的出拳习惯:①第一局不出“剪刀”;②连续两局的出拳方法一定不一样,即如果本局出“剪刀”,则下局将不再出“剪刀”,而是选“石头”、“布”中的某一个.假设专家的分析是正确的,甲根据专家的分析出拳,保证每一局都不输给乙.在最多5局的比赛中,谁胜的局数多,谁获胜.游戏结束的条件是:一方胜3局或赛满5局,用X表示游戏结束时的游戏局数,求X的分布列和期望.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com