题目列表(包括答案和解析)
已知函数
(其中a,b为实常数)。
（Ⅰ）讨论函数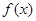
的单调区间：
（Ⅱ）当
时，函数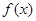有三个不同的零点，证明：
：
（Ⅲ）若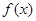在区间
上是减函数，设关于x的方程
的两个非零实数根为
，
。试问是否存在实数m,使得
对任意满足条件的a及t
恒成立？若存在，求m的取值范围；若不存在，请说明理由。
已知函数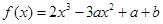
(其中a,b为实常数)。
（Ⅰ）讨论函数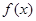
的单调区间：
（Ⅱ）当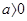
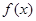时，函数有三个不同的零点，证明：
：
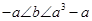（Ⅲ）若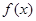在区间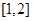
上是减函数，设关于x的方程
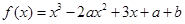的两个非零实数根为
，
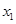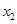。试问是否存在实数m,使得
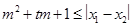对任意满足条件的a及t
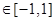恒成立？若存在，求m的取值范围；若不存在，请说明理由。
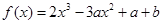(其中a,b为实常数)。
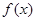的单调区间：
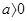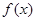时，函数有三个不同的零点，证明：
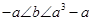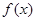：在区间
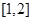上是减函数，设关于x的方程
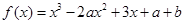的两个非零实数根为
，
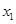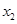。试问是否存在实数m,使得
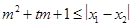对任意满足条件的a及t
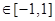恒成立？若存在，求m的取值范围；若不存在，请说明理由。一、选择题：每小题5分，满分60分.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
A
A
C
D
B
A
C
C
A
D
B
二、填空题：每小题4分，满分16分.
13． 
14． 1359
15． 
16．
三、解答题
17．解：(Ⅰ) 0.525 ……… 4分
(Ⅱ)
0
55
60
65
70
75
80
85
90
95
100
P
………12分
18．解：（Ⅰ）由
，得
，
；
所以数列
只有三项：
，
，
……… 3分
（Ⅱ）由题设
，解得
或
即当或时得到无穷的常数列
或
；……… 6分
（Ⅲ）解不等式
，得
或
……… 9分
当时，
，
，与
矛盾；
当时，
，依此类推，可得
综上， ………12分
19．解：（Ⅰ）由几何体的三视图可知，底面
是边长为
的正方形，
面，
∥
，
．
为
的中点
，
又
面
……… 4分
（Ⅱ）取
的中点
，
与
的交点为
，
∥，
∥，故BEMN为平行四边形
∥
∥面
……… 8分
（Ⅲ）分别以
为
轴建立坐标系，
则
，
，
为的中点，
面
为面的法向量，
，
设平面的法向量为
，
则
，与
的夹角为
………11分
面
与面
所成的二面角（锐角）的余弦值为
………12分
20．解：（Ⅰ）设
，由题设得
，整理得
其中
，
故点A的轨迹（含点B、C）M方程为． ……… ４分
（Ⅱ）过点
，与
轴平行的切线存在，此时
， ……… 6分
设过点，斜率为
的切线方程为
，于是
整理得 
此方程有重根
即
即
解得
且
………10分
所求切线方程为
………12分
21．解：由
，得
，
于是
……… 3分
考察函数
，可知
……… 6分
在
上， 
和
变化情况如下表：
x
0
0
－
－
０
＋
＋
０
－
０
＋
0
↓
↓
１
↑
↑
０
↓
↑
……… 9分
从而，可得圆方程不同实数根的个数如下：
当
或
或
时，有2个；当
时，有3个；
当
时，有4个；当
时，有0个；
当
时，有1个． ………12分
22解:（Ⅰ）连结OF．∵DF切⊙O于F，∴∠OFD=90°．∴∠OFC+∠CFD=90°．
∵OC=OF，∴∠OCF=∠OFC．∵CO⊥AB于O，∴∠OCF+∠CEO=90°．
∴∠CFD=∠CEO=∠DEF，∴DF=DE．
∵DF是⊙O的切线,∴DF2=DB?DA．∴DE2=DB?DA. ……… 5分
（Ⅱ）
，CO=
， 
．
∵CE?EF= AE?EB= （+2）（-2）=8，∴EF=2． ………10分
23解：（Ⅰ）设M为圆上一点，坐标为
，则∠
或
，
由余弦定理得
∴极坐标方程为
……… 5分
（Ⅱ）
的普通方程为
，圆心
，半径
．
的普通方程为
．
因为圆心到直线的距离为
，
所以与只有一个公共点． ………10分
24．解：（Ⅰ）由绝对值不等式性质知：
对
恒成立
故
的解集为
，只须
既可
的取值范围是
……… 5分
（Ⅱ）由（Ⅰ）知实数的最大值为3，当
时，
成立
证明如下：（利用分析法）要使成立
只须
等价于 
等价于 
等价于
，而显然成立，
以上每一步均可逆推，故所证明不等式成立。 ………10
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com