
题目列表(包括答案和解析)
(本小题满分14分) 已知函数![]() 及正整数数列
及正整数数列![]() . 若
. 若![]() ,且当
,且当![]() 时,有
时,有![]() ; 又
; 又![]() ,
,![]() ,且
,且![]() 对任意
对任意![]() 恒成立. 数列
恒成立. 数列![]() 满足:
满足:![]() .
.
(1) 求数列![]() 及
及![]() 的通项公式;
的通项公式;
(2) 求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3) 证明存在![]() ,使得
,使得![]() 对任意
对任意![]() 均成立.
均成立.
(本小题满分14分)
如图,正四棱柱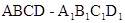 中,
中,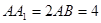 ,点
,点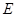 在
在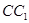 上且
上且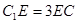 .
.

(1) 证明: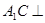 平面
平面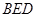 ;
;
(2) 求二面角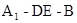 的余弦值.
的余弦值.
(本小题满分14分)
将数列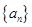 中的所有项按每一行比上一行多一项的规则排成如下数表:
中的所有项按每一行比上一行多一项的规则排成如下数表:
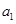
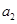
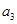
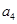
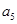
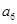
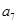
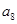
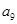
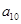
………………………
记表中的第一列数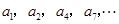 构成的数列为
构成的数列为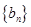 ,
,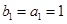 .
.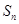 为数列
为数列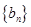 的前
的前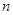 项和,且满足
项和,且满足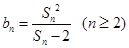 .
.
(1)证明: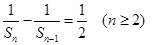 ;
;
(2)求数列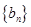 的通项公式;
的通项公式;
(3)上表中,若从第三行起,每一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当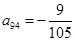 时,求上表中第
时,求上表中第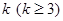 行所有项的和.
行所有项的和.
(本小题满分14分)有人玩掷正四面体骰子走跳棋的游戏,已知正四面体骰子四个面上分别印有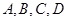 ,棋盘上标有第0站、第1站、第2站、…、第100站.一枚棋子开始在第0站,棋手每掷一次骰子,若掷出后骰子为
,棋盘上标有第0站、第1站、第2站、…、第100站.一枚棋子开始在第0站,棋手每掷一次骰子,若掷出后骰子为 面,棋子向前跳2站,若掷出后骰子为
面,棋子向前跳2站,若掷出后骰子为 中的一面,则棋子向前跳1站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为
中的一面,则棋子向前跳1站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为 (
(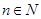 ).
).
(Ⅰ)求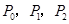 ;
;
(Ⅱ)求证: ;
;
(Ⅲ)求玩该游戏获胜的概率.
(本小题满分14分)如图,正三棱柱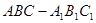 的侧棱长和底面边长均为
的侧棱长和底面边长均为 ,
,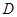 是
是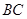 的中点.
的中点.
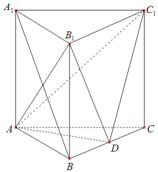
(Ⅰ)求证: 平面
平面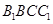 ;
;
(Ⅱ)求证: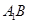 ∥平面
∥平面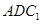 ;
;
(Ⅲ)求三棱锥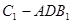 的体积.
的体积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com