本小题12分）

调查某地区老年人是否需要志愿者帮助，用简单随机抽样方法从该地调查500位老年人，结果如下：

性别 是否需要	男	女
需要	40	30
不需要	160	270

①估计该地区老年人中，需要志愿者提供帮助的老年人的比例。

②能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关？

附：

P（K2≥k）	0.050	0.010	0.001
k	3.841	6.635	10.828

 

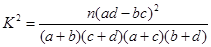
本小题12分）
调查某地区老年人是否需要志愿者帮助，用简单随机抽样方法从该地调查500位老年人，结果如下：

性别 是否需要	男	女
需要	40	30
不需要	160	270

①估计该地区老年人中，需要志愿者提供帮助的老年人的比例。
②能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关？
附：

P（K2≥k）	0.050	0.010	0.001
k	3.841	6.635	10.828

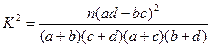
(本小题12分)

随机抽取某中学甲乙两个班级各10名同学,测量他们的身高(单位:cm),获得的数据如下:

甲:182  170  171  179  179  162  163  168  168  158

乙:181  170  173  176  178  179  162  165  168  159

(1)根据上述的数据作出茎叶图表示;

(2)判断哪个班级的平均身高较高,并求出甲班的方差;

(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,身高176cm的同学被抽中的概率是多少?

 

(本小题12分)

随机调查某社区80个人,以研究这一社区居民在20:00-22:00时间段的休闲方式与性别有关系,得到下面的数据表:

休闲方式 性别	看电视	看书	合计
男	10	50	60
女	10	10	20
合计	20	60	80

(1)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量,求的分布列和期望;

(2)根据以上数据,能否有99%的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?

参考公式: ,其中

参考数据:

	0.15	0.10	0.05	0.025	0.010
	2.072	2.706	3.841	5.042	6.635

 

(本小题12分) 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.

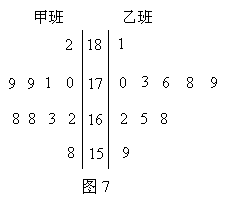(1)根据茎叶图判断哪个班的平均身高较高;       

(2)计算甲班的样本方差

(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.