（本小题满分13分）

。，轮船位于港口O北偏西且与该港口相距20海里的A处，并以30海里/小时的航行速度沿正东方向匀速行驶。假设该小船沿直线方向以海里/小时的航行速度匀速行驶，经过t小时与轮船相遇。

（1）若希望相遇时小艇的航行距离最小，则小艇航行速度的大小应为多少？

（2）假设小艇的最高航行速度只能达到30海里/小时，试设计航行方案（即确定航行方向与航行速度的大小），使得小艇能以最短时间与轮船相遇，并说明理由。

（（本小题满分13分）

设数列为等差数列，且a₅=14，a₇=20。

（I）求数列的通项公式；

（II）若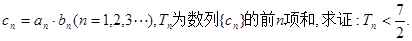

(本小题满分13分)某创业投资公司拟投资开发某种新能源产品，估计能获得10万元～1000万元的投资收益.现准备制定一个对科研课题组的奖励方案：奖金y（单位：万元）随投资收益x（单位：万元）的增加而增加，且奖金不超过9万元，同时奖金不超过投资收益的20%.（Ⅰ）若建立函数模型制定奖励方案，试用数学语言表述公司对奖励函数模型的基本要求；（Ⅱ）现有两个奖励函数模型：(1)y＝；(2)y＝4lgx－3.试分析这两个函数模型是否符合公司要求？

(本小题满分13分)为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层．某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用C（单位：万元）与隔热层厚度（单位：cm）满足关系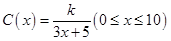：，若不建隔热层，每年能源消耗费用为8万元．设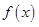为隔热层建造费用与20年的能源消耗费用之和．

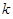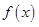（Ⅰ）求的值及的表达式；

（Ⅱ）隔热层修建多厚时，总费用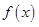达到最小，并求最小值．

(本小题满分13分)

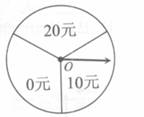
    某商场为吸引顾客消费推出一项优惠活动．活动规则如下：消费每满100元可以转动如图所示的圆盘一次，其中O为圆心，且标有20元、10元、0元的三部分区域面积相等，假定指针停在任一位置都是等可能的．当指针停在某区域时，返相应金额的优惠券。(例如：某顾客消费了218元，第一次转动获得了20元，第二次获得了10元，则其共获得了30元优惠券。)顾客甲和乙都到商场进行了消费，并按照规则参与了活动．

  （I）若顾客甲消费了128元，求他获得优惠券面额大于0元的概率?

  （II）若顾客乙消费了280元，求他总共获得优惠券金额不低于20元的概率?