
题目列表(包括答案和解析)
、(本小题满分13分).在正方体ABCD-A1B1C1D1中,M、N、P分别是CC1、B1C1、C1D1的中点.(温馨提示:该题要在答题卡上作图,否则扣分)。
(1) 求异面直线PN、AC所成角; (2) 求证:平面MNP∥平面A1BD.
(本小题满分13分)对于在区间[m,n]上有意义的两个函数![]() 与
与![]() ,如果对任意
,如果对任意![]() [m,n]均有
[m,n]均有![]() ,称
,称![]() 与
与![]() 在[m,n]上是接近的,否则称
在[m,n]上是接近的,否则称![]() 与
与![]() 在[m,n]上是非接近的,现有两个函数
在[m,n]上是非接近的,现有两个函数![]() 与
与![]() (a>0,a≠1),给定区间[a+2,a+3].(1)若
(a>0,a≠1),给定区间[a+2,a+3].(1)若![]() 与
与![]() 在给定区间[a+2,a+3]上都有意义,求a的取值范围;(2)讨论
在给定区间[a+2,a+3]上都有意义,求a的取值范围;(2)讨论![]() 与
与![]() 在[a+2,a+3]上是否是接近的.
在[a+2,a+3]上是否是接近的.
(本小题满分13分) 为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶 和外墙需要建造隔热层.
和外墙需要建造隔热层.
某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度 (单位:cm)满足关系:
(单位:cm)满足关系: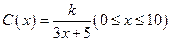 ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设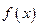 为隔热
为隔热
层建造费用与20年的能源消耗费用之和.(Ⅰ)求 的值及
的值及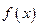 的表达式;(Ⅱ)隔热层修建多厚时,总费用
的表达式;(Ⅱ)隔热层修建多厚时,总费用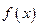 达到最小?并求最小值。
达到最小?并求最小值。
(本小题满分13分)
数列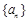 的首项
的首项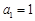 ,前
,前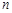 项和为
项和为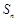 ,满足关系
,满足关系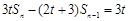 (
(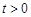 ,
,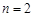 ,3,4…)
,3,4…)
(1)求证:数列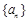 为等比数列;
为等比数列;
(2)设数列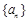 的公比为
的公比为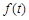 ,作数列
,作数列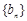 ,使
,使 ,
, .(
.(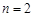 ,3,4…)求
,3,4…)求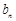
(3)求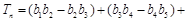 …
… 的值
的值
(2009安徽卷理)(本小题满分13分)
点![]() 在椭圆
在椭圆![]() 上,
上,![]() 直线
直线![]() 与直线
与直线![]() 垂直,O为坐标原点,直线OP的倾斜角为
垂直,O为坐标原点,直线OP的倾斜角为![]() ,直线
,直线![]() 的倾斜角为
的倾斜角为![]() .
.
(I)证明: 点![]() 是椭圆
是椭圆![]() 与直线
与直线![]() 的唯一交点;
的唯一交点; ![]()
![]()
(II)证明:![]() 构成等比数列.
构成等比数列.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com