
题目列表(包括答案和解析)
(本小题满分14分)
因发生意外交通事故,一辆货车上的某种液体泄漏到一渔塘中.为了治污,根据环保部门的建议,现决定在渔塘中投放一种可与污染液体发生化学反应的药剂.已知每投放![]() ,且
,且![]() 个单位的药剂,它在水中释放的浓度
个单位的药剂,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (天)变化的函数关系式近似为
(天)变化的函数关系式近似为![]() ,其中
,其中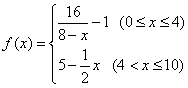 .
.
若多次投放,则某一时刻水中的药剂浓度为每次投放的药剂在相应时刻所释放的浓度之和.根据经验,
当水中药剂的浓度不低于4(克/升)时,它才能起到有效治污的作用.
(Ⅰ)若一次投放4个单位的药剂,则有效治污时间可达几天?
(Ⅱ)若第一次投放2个单位的药剂,6天后再投放![]() 个单位的药剂,要使接下来的4天中能够持续有效治污,试求
个单位的药剂,要使接下来的4天中能够持续有效治污,试求![]() 的最小值(精确到0.1,参考数据:
的最小值(精确到0.1,参考数据:![]() 取1.4).
取1.4).
(本小题满分14分)
选修4-2:矩阵及其变换
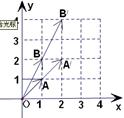
(1)如图,向量 被矩阵M作用后分别变成
被矩阵M作用后分别变成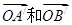 ,
,
(Ⅰ)求矩阵M;
(Ⅱ)并求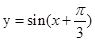 在M作用后的函数解析式;
在M作用后的函数解析式;
选修4-4:坐标系与参数方程
( 2)在直角坐标系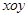 中,直线
中,直线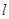 的参数方程为
的参数方程为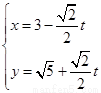 (
(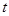 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系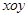 取相同的长度单位,且以原点
取相同的长度单位,且以原点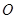 为极点,以
为极点,以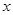 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆 的方程为
的方程为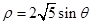 。
。
(Ⅰ)求圆 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设圆 与直线
与直线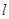 交于点
交于点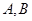 。若点
。若点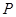 的坐标为(3,
的坐标为(3,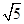 ),求
),求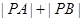 。
。
选修4-5:不等式选讲
(3)已知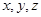 为正实数,且
为正实数,且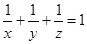 ,求
,求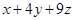 的最小值及取得最小值时
的最小值及取得最小值时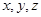 的值.
的值.
(本小题满分14分)
已知函数![]() 为实常数).
为实常数).
(I)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最小值;
上的最小值;
(Ⅱ)若方程![]() (其中
(其中![]() )在区间
)在区间![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)证明:![]() (参考数据:
(参考数据:![]() )
)
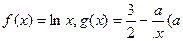 为实常数).
为实常数).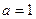 时,求函数
时,求函数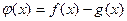 在
在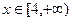 上的最小值;
上的最小值;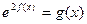 (其中
(其中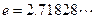 )在区间
)在区间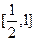 上有解,求实数
上有解,求实数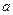 的取值范围;
的取值范围;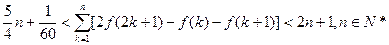 (参考数据:
(参考数据: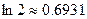 )
)((本小题满分14分)
已知函数 为实常数).
为实常数).
(I)当 时,求函数
时,求函数 在
在 上的最小值;
上的最小值;
(Ⅱ)若方程 (其中
(其中 )在区间
)在区间 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
(Ⅲ)证明: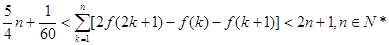 (参考数据:
(参考数据: )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com