
题目列表(包括答案和解析)
(本题满分15分)已知函数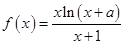
(Ⅰ)若函数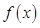 在
在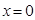 处取到极值,求
处取到极值,求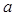 的值.
的值.
(Ⅱ)设定义在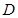 上的函数
上的函数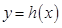 在点
在点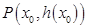 处的切线方程为
处的切线方程为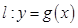 ,若
,若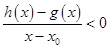 在
在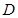 内恒成立,则称
内恒成立,则称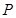 为函数的
为函数的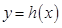 的“HOLD点”.当
的“HOLD点”.当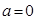 时,试问函数
时,试问函数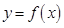 是否存在“HOLD点”,若存在,请至少求出一个“HOLD点”的横坐标;若不存在,请说明理由.
是否存在“HOLD点”,若存在,请至少求出一个“HOLD点”的横坐标;若不存在,请说明理由.
(本题满分15分)已知函数 .
.
(Ⅰ)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)是否存在实数 ,使得函数
,使得函数 有唯一的极值,且极值大于
有唯一的极值,且极值大于 ?若存在,,求
?若存在,,求 的取值
的取值
范围;若不存在,说明理由;
(Ⅲ)如果对 ,总有
,总有 ,则称
,则称 是
是 的凸
的凸
函数,如果对 ,总有
,总有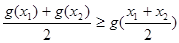 ,则称
,则称 是
是 的凹函数.当
的凹函数.当 时,利用定义分析
时,利用定义分析 的凹凸性,并加以证明。
的凹凸性,并加以证明。
(本题满分15分)设M是由满足下列条件的函数![]() 构成的集合:“①方程
构成的集合:“①方程![]() 有实数根;②函数
有实数根;②函数![]() 的导数
的导数![]() 满足
满足![]() ”
”
(I)证明:函数![]() 是集合M中的元素;
是集合M中的元素;
(II)证明:函数![]() 具有下面的性质:对于任意
具有下面的性质:对于任意![]()
![]() ,都存在
,都存在![]() ,使得等式
,使得等式![]() 成立。
成立。
(III)若集合M中的元素![]() 具有下面的性质:若
具有下面的性质:若![]() 的定义域为D,则对于任意[m,n]
的定义域为D,则对于任意[m,n]![]() ,都存在
,都存在![]() ,使得等式
,使得等式![]() 成立。试用这一性质证明:对集合M中的任一元素
成立。试用这一性质证明:对集合M中的任一元素![]() ,方程
,方程![]() 只有一个实数根。
只有一个实数根。
(本题满分15分)已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性即没患病.下面是两种化验方法:
方案甲:逐个化验,直到能确定患病动物为止.
方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验.
(Ⅰ)分别求依方案甲所需化验次数与依方案乙所需化验次数的分布列;
(Ⅱ)![]() 表示依方案乙所需化验次数,求
表示依方案乙所需化验次数,求![]() 的期望.。
的期望.。
(本题满分15分)
经过长期的观测得到:在交通繁忙时段,某公路段汽车的车流量y(千辆/小时)与汽车的平均速度v(千米/小时)之间的函数关系为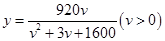 .
.
(1)在该时段内,当汽车的平均速度v为多少时,车流量最大?最大车流量为多少?
(精确到0.1千辆/小时)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com