(本题满分14分)

如图,圆锥的顶点是S，底面中心为O.OC是与底面直径AB垂直的一条半径，D是母线SC的中点.

（1）求证：BC与SA不可能垂直.

（2）设圆锥的高为4，异面直线AD与BC所成角的余弦值为，求圆锥的体积.

（文科做）（本题满分14分）如图，在长方体

ABCD—A₁B₁C₁D₁中，AD=AA₁=1，AB=2，点E在棱AB上移动.

（1）证明：D₁E⊥A₁D;

（2）当E为AB的中点时，求点E到面ACD₁的距离；

（3）AE等于何值时，二面角D₁—EC－D的大小为.　　　　　　　　　　　　　　　　　　　　　　

（理科做）(本题满分14分)

     如图，在直三棱柱ABC – A₁B₁C₁中，∠ACB = 90°，CB = 1，

CA =，AA₁ =，M为侧棱CC₁上一点，AM⊥BA₁．

   （Ⅰ）求证：AM⊥平面A₁BC；

   （Ⅱ）求二面角B – AM – C的大小；

   （Ⅲ）求点C到平面ABM的距离．

(本题满分14分)

如图所示，在正三棱柱ABC -A₁B₁C₁中，底面边长和侧棱长都是2，D是侧棱CC₁上任意一点，E是A₁B₁的中点。

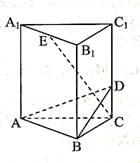
（I）求证：A₁B₁//平面ABD；

（II）求证：AB⊥CE；

（III）求三棱锥C-ABE的体积。

(本题满分14分)

如图1，在平面内，ABCD是的菱形，ADD``A<sub>1</sub>和CD D`C<sub>1</sub>都是正方形．将两个正方形分别沿AD，CD折起，使D``与D`重合于点D₁ .设直线l过点B且垂直于菱形ABCD所在的平面，点E是直线l上的一个动点，且与点D₁位于平面ABCD同侧（图2）．

(Ⅰ) 设二面角E – AC – D₁的大小为q，若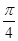£ q £ ，求线段BE长的取值范围；

(Ⅱ)在线段上存在点，使平面平面，求与BE之间满足的关系式，并证明：当0 < BE < a时，恒有< 1．

 (本题满分14分) 如图，某住宅小区的花园平面图呈圆心角为120°、半径为r的扇形AOB，花园的两个出入口设置在点A及点C处，且花园里有一条平行于BO的小路CD。某人散步从C沿CD走到D用了4分钟，从D沿DA走到A用了2分钟，假设此人散步的速度为每分钟40米。

（1）求该扇形的半径r的长；

（2）今从点O开始，先沿OA方向、然后折向与DC平行的方向在花园内铺一灌溉水管，求该水管的最大长度.