
题目列表(包括答案和解析)
.(本小题满分12分)
如图4所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中
的数学成绩.乙组记录中有一个数据模糊,无法确认,在图中以 表示.
表示.
已知甲、乙两个小组的数学成绩的平均分相同.
(1)求 的值;
的值;
(2)求乙组四名同学数学成绩的方差;
(3)分别从甲、乙两组同学中各随机选取一名同学,记这两名同学数学
成绩之差的绝对值为 ,求随机变量
,求随机变量 的分布列和均值(数学期望).
的分布列和均值(数学期望).

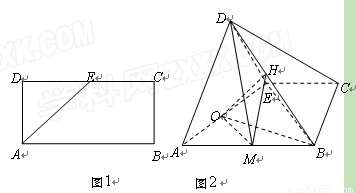
(本小题满分12分)如图1所示,在矩形 中,
中,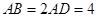 ,
,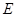 为
为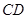 的中点,沿
的中点,沿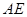 将
将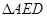 折起,如图2所示,在图2中,
折起,如图2所示,在图2中, 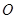 、
、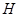 、
、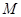 分别为
分别为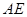 、
、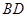 、
、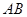 的中点,且
的中点,且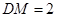 .
.
(Ⅰ)求证: 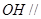 平面
平面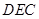 ;
;
(Ⅱ) 求证:面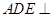 面
面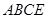 ;
;
(Ⅲ)求三棱锥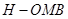 的体积.
的体积.
(本小题满分12分)
如图一所示,边长为1的正方体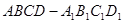 中,
中, 分别为
分别为 的中点。
的中点。
(Ⅰ)证明: ;
;
(Ⅱ)若 为
为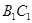 的中点,证明:
的中点,证明: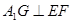 ;
;
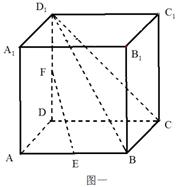
(Ⅲ)如图二所示为一几何体的展开图,沿着图中虚线将它们折叠起来,所得几何体的体积为 ,若正方体
,若正方体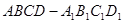 的体积为
的体积为 ,求
,求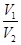 的值。
的值。
(本小题满分12分)如下图所示,某海轮以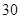 海里/小时的速度航行,在
海里/小时的速度航行,在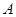 点测得海面上油井
点测得海面上油井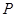 在南偏东
在南偏东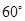 ,向北航行
,向北航行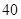 分钟后到达
分钟后到达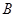 点,测得油井
点,测得油井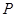 在南偏东
在南偏东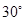 ,海轮改为北偏东
,海轮改为北偏东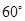 的航向再行驶
的航向再行驶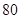 分钟到达
分钟到达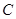 点,求
点,求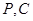 间的距离.
间的距离.
(本小题满分12分)如下图(3),在四棱锥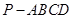 中,四边形
中,四边形 是平行四边形,
是平行四边形,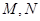 分别是
分别是 的中点,求证:
的中点,求证: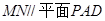 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com