（本小题满分12分）

　　　已知函数。

　　（Ⅰ）设{a_n}是正数组成的数列，前n项和为S_n，其中a₁=3，若点 (n∈N*)在函数y=f′(x)的图象上，求证：点（n, S_n）也在y=f′(x)的图象上；

　　（Ⅱ）求函数f(x)在区间（a-1,a）内的极值。

（本小题满分12分）已知定义在R上的单调函数，存在实数，使得对于任意实数，总有恒成立。
(Ⅰ）求的值；(Ⅱ)若,且对任意,有，求{a_n}的通项公式；
(Ⅲ)若数列{b_n}满足，将数列{b_n}的项重新组合成新数列，具体法则如下：，……，求证：。

（本小题满分12分）

在数列{a_n}中，a₁=2,a₂=8，且已知函数（）在x=1时取得极值.(Ⅰ)求证:数列{a_n+1—2a_n}是等比数列,（Ⅱ）求数列的通项a_n；（Ⅲ）设，且对于恒成立，求实数m的取值范围．

（本小题满分12分）

 (理科)已知数列 {2 ⁿ•a_n} 的前 n 项和 S_n = 9－6n.

 (I)    求数列 {a_n} 的通项公式；

(II)    设 b_n = n·(2－log ₂ )，求数列 { } 的前 n 项和T_n.

（文科）已知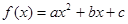，且f(0)=8及f(x+1)－f(x)＝－2x+1。

 (1)求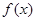的解析式；

 (2)求函数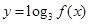的单调递减区间及值域．

（本小题满分12分）

　　　已知函数。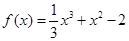

　　（Ⅰ）设{a_n}是正数组成的数列，前n项和为S_n，其中a₁=3，若点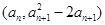 (n∈N*)在函数y=f′(x)的图象上，求证：点（n, S_n）也在y=f′(x)的图象上；

　　（Ⅱ）求函数f(x)在区间（a-1,a）内的极值。