
题目列表(包括答案和解析)
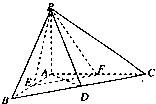
如图,PC⊥平面ABC,∠ACB=90°,D为AB中点,AC=BC=PC=2.
(I)求证:AB⊥平面PCD;
(II)求异面直线PD与BC所成的角的余弦值;
(III)求点C到平面PAD的距离.

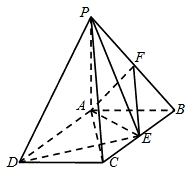 如图,已知PA⊥平面ABCD,ABCD是矩形,PA=AB=1,
如图,已知PA⊥平面ABCD,ABCD是矩形,PA=AB=1, ,F是PB中点,点E在BC边上.
,F是PB中点,点E在BC边上.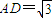 ,F是PB中点,点E在BC边上.
,F是PB中点,点E在BC边上.
 如图,在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=
如图,在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=| π | 2 |
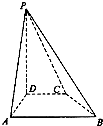
| AD |
一、选择题(本大题12小题,每小题5分,共60分。在每小题经出的四个选项中,只有一项是符合题目要求的。))
1―5DCBAC 6―10BCADB 11―12BB
二、填空题(本大题共4个小题,每小题5分,共20分。将符合题意的答案填在题后的横线上)
13.2 14.70 15..files\image134.gif) 16.
16..files\image136.gif)
三、解答题:本大题共6个小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.解:(I).files\image138.gif) …………4分
…………4分
.files\image140.gif)
.files\image142.gif)
.files\image144.gif) …………6分
…………6分
(II).files\image146.gif)
.files\image148.gif)
.files\image150.gif)
.files\image152.gif) …………8分
…………8分
.files\image154.gif)
.files\image156.gif)
.files\image158.gif) …………10分
…………10分
18.解:(I)设通晓英语的有.files\image160.gif) 人,
人,
且.files\image162.gif) …………1分
…………1分
则依题意有:.files\image164.gif)
.files\image166.gif) …………3分
…………3分
所以,这组志愿者有.files\image168.gif) 人。…………4分
人。…………4分
(II)所有可能的选法有.files\image170.gif) 种…………5分
种…………5分
A被选中的选法有.files\image172.gif) 种…………7分
种…………7分
A被选中的概率为.files\image174.gif) …………8分
…………8分
(III)用N表示事件“B,C不全被选中”,则.files\image176.gif) 表示事件“B,C全被选中”……10分
表示事件“B,C全被选中”……10分
则.files\image178.gif) …………11分
…………11分
所以B和C不全被选中的概率为.files\image180.gif) ……12分
……12分
说明:其他解法请酌情给分。
|