
题目列表(包括答案和解析)
(14分)已知函数f(x)=![]() 的图像在点P(0,f(0))处的切线方程为y=3x-2
的图像在点P(0,f(0))处的切线方程为y=3x-2
(Ⅰ)求实数a,b的值;
(Ⅱ)设g(x)=f(x)+![]() 是[
是[![]() )上的增函数。
)上的增函数。
(i)求实数m的最大值;
(ii)当m取最大值时,是否存在点Q,使得过点Q的直线若能与曲线y=g(x)围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,写出点Q的坐标(可以不必说明理由);若不存在,说明理由。
(本小题满分12分)
设椭圆 的离心率
的离心率 ,右焦点到直线
,右焦点到直线 的距离
的距离
 为坐标原点。
为坐标原点。
(I)求椭圆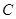 的方程;
的方程;
(II)过点 作两条互相垂直的射线,与椭圆
作两条互相垂直的射线,与椭圆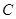 分别交于
分别交于 两点,证明点
两点,证明点 到直线
到直线 的距离为定值,并求弦
的距离为定值,并求弦 长度的最小值.
长度的最小值.
(本小题满分12分)
设椭圆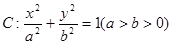 的离心率
的离心率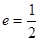 ,右焦点到直线
,右焦点到直线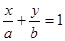 的距离
的距离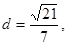 O为坐标原点。
O为坐标原点。
(I)求椭圆C的方程;
(II)过点O作两条互相垂直的射线,与椭圆C分别交于A,B两点,证明点O到直线AB的距离为定值,并求弦AB长度的最小值。
(本小题满分14分)
设数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意的正整数
,对任意的正整数![]() ,都有点
,都有点![]() 在直线y=5x+1上,记
在直线y=5x+1上,记![]() (n∈N*)。(I)求数列
(n∈N*)。(I)求数列![]() 的通项公式;(II)记
的通项公式;(II)记![]() ,设
,设![]() ,求证:对任意正整数
,求证:对任意正整数![]() 都有
都有![]() ;(III)设
;(III)设![]() 。已知正实数
。已知正实数![]() 满足:对任意正整数
满足:对任意正整数![]() 恒成立,求
恒成立,求![]() 的最小值。
的最小值。
 的离心率
的离心率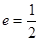 ,右焦点到直线
,右焦点到直线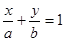 的距离
的距离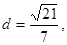
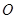 为坐标原点。
为坐标原点。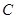 的方程;
的方程;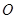 作两条互相垂直的射线,与椭圆
作两条互相垂直的射线,与椭圆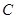 分别交于
分别交于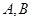 两点,证明点
两点,证明点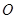 到直线
到直线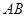 的距离为定值,并求弦
的距离为定值,并求弦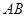 长度的最小值.
长度的最小值.
一、选择题(本大题12小题,每小题5分,共60分。在每小题经出的四个选项中,只有一项是符合题目要求的。))
1―5DCBAC 6―10BCADB 11―12BB
二、填空题(本大题共4个小题,每小题5分,共20分。将符合题意的答案填在题后的横线上)
13.2 14.70 15..files\image134.gif) 16.
16..files\image136.gif)
三、解答题:本大题共6个小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.解:(I).files\image138.gif) …………4分
…………4分
.files\image140.gif)
.files\image142.gif)
.files\image144.gif) …………6分
…………6分
(II).files\image146.gif)
.files\image148.gif)
.files\image150.gif)
.files\image152.gif) …………8分
…………8分
.files\image154.gif)
.files\image156.gif)
.files\image158.gif) …………10分
…………10分
18.解:(I)设通晓英语的有.files\image160.gif) 人,
人,
且.files\image162.gif) …………1分
…………1分
则依题意有:.files\image164.gif)
.files\image166.gif) …………3分
…………3分
所以,这组志愿者有.files\image168.gif) 人。…………4分
人。…………4分
(II)所有可能的选法有.files\image170.gif) 种…………5分
种…………5分
A被选中的选法有.files\image172.gif) 种…………7分
种…………7分
A被选中的概率为.files\image174.gif) …………8分
…………8分
(III)用N表示事件“B,C不全被选中”,则.files\image176.gif) 表示事件“B,C全被选中”……10分
表示事件“B,C全被选中”……10分
则.files\image178.gif) …………11分
…………11分
所以B和C不全被选中的概率为.files\image180.gif) ……12分
……12分
说明:其他解法请酌情给分。
|