
题目列表(包括答案和解析)
(本小题满分12分)
| 第一批次 | 第二批次 | 第三批次 | |
| 女教职工 | 196 | x | y |
| 男教职工 | 204 | 156 | z |
某学校共有教职工900人,分成三个批次进行继续教育培训,在三个批次中男、女教职工人数如左表所示. 已知在全体教职工中随机抽取1名,抽到第二批次中女教职工的概率是0.16 .
(1)求![]() 的值;
的值;
(2)现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查, 问应在第三批次中
抽取教职工多少名?
(3)已知![]() ,求第三批次中女教职工比男教职工多的概率.
,求第三批次中女教职工比男教职工多的概率.
(本小题满分12分,第一问4分,第二问8分)
如图(20),椭圆的中心为原点O,离心率 ,一条准线的方程为
,一条准线的方程为 。
。
(Ⅰ)求该椭圆的标准方程。
(Ⅱ)设动点P满足 ,其中M,N是椭圆上的点。直线OM与ON的斜率之积为
,其中M,N是椭圆上的点。直线OM与ON的斜率之积为 。问:是否存在两个定点
。问:是否存在两个定点 ,使得
,使得 为定值。若存在,求
为定值。若存在,求 的坐标;若不存在,说明理由。
的坐标;若不存在,说明理由。
(本小题满分12分)
设等差数列 第10项为24,第25项为
第10项为24,第25项为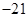 ,
,
(1)求这个数列的通项公式;
(2)设 为其前n项和,求使
为其前n项和,求使 取最大值时的n值。
取最大值时的n值。
(本小题满分12分)
设等差数列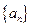 第10项为24,第25项为
第10项为24,第25项为 ,
,
(1)求这个数列的通项公式;
(2)设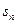 为其前n项和,求使
为其前n项和,求使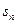 取最大值时的n值。
取最大值时的n值。
(本小题满分12分)(文科做前两问;理科全做.)
某会议室用3盏灯照明,每盏灯各使用节能灯棍一只,且型号相同.假定每盏灯能否正常照明只与灯棍的寿命有关,该型号的灯棍寿命为1年以上的概率为0.8,寿命为2年以上的概率为0.3,从使用之日起每满1年进行一次灯棍更换工作,只更换已坏的灯棍,平时不换.
(I)在第一次灯棍更换工作中,求不需要更换灯棍的概率;
(II)在第二次灯棍更换工作中,对其中的某一盏灯来说,求该灯需要更换灯棍的概率;
(III)设在第二次灯棍更换工作中,需要更换的灯棍数为ξ,求ξ的分布列和期望.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com