查看答案和解析>>

查看答案和解析>>

经过点F（0，1）且与直线y=-1相切的动圆的圆心轨迹为M．点A、D在轨迹M上，且关于y轴对称，过线段AD（两端点除外）上的任意一点作直线，使直线与轨迹M在点D处的切线平行，设直线与轨迹M交于点B、C．
（1）求轨迹M的方程；
（2）证明：∠BAD=∠CAD；
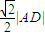（3）若点D到直线AB的距离等于，且△ABC的面积为20，求直线BC的方程．

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

一．选择题：CDDA  DDBA  BBDC ．

二．填空题：（13）60，（14），（15），（16）①②④ ．

三．解答题：

（17）解：（Ⅰ）∵

．                 ………3分

∴令，        ………4分

∴的递减区间是，；              ………5分

令，           ………6分

∴的递增区间是，．              ………7分

（Ⅱ）∵，∴，                     ………8分

      又，所以，根据单位圆内的三角函数线

可得．                                     ………10分

（18）解：由题意，                                       ………1分

，                                        ………2分

，                              ………4分

，                            ………6分

，                      ………8分

所以的分布列为：                                    

…

………9分

．          ………12分

（19）解：（Ⅰ）由题设可知，．                    ………1分

∵，，

∴，                                 ………3分

∴

，              ………5分

∴ ．                                             ………6分

（Ⅱ）设．                        ………7分

显然，时，，                                       ………8分

又， ∴当时，，∴，                       

当时，，∴，                             ………9分

当时，，∴，                        ………10分

当时，恒成立，

∴恒成立，                               ………11分

∴存在，使得．                                 ………12分

（20）解：（Ⅰ）∵PA⊥平面ABCD，PC⊥AD，∴AC⊥AD．                 ………1分

设AB=1，则AC=，CD=2．                                     ………2分

设F是AC与BD的交点，∵ABCD为梯形，

∴△ABF～△CDF， ∴DF：FB=2：1，                               ………3分

又PE：EB=2：1，∴DF：FB=PE：EB，∴EF∥PD，                   ………5分

又EF在平面ACE内，∴PD∥平面ACE．                             ………6分

（Ⅱ）以A为坐标原点，AB为y轴，AP为z轴建立空间直角坐标系，如图．

设AB=1，则，，，，             ………7分

则，，，，     ………8分

设，∵，，∴，  …9分

设，∵，，∴， …10分

∴，      ………11分

∴二面角A-EC-P的大小为．………12分

注：学生使用其它解法应同步给分．

（21）解：（Ⅰ）设所求的椭圆E的方程为，                ………1分

、，将代入椭圆得，     ………2分

∵，又，∴ ，                        ………3分

∴， ………4分，       ，              ………5分

∴所求的椭圆E的方程为．                                ………6分

（Ⅱ）设、，则，，          ………7分

又设MN的中点为，则以上两式相减得：，         ………8分

∴，………9分，     ，                  ………10分

又点在椭圆内，∴，                               ………11分

即，，∴．                         ………12分

注：学生使用其它解法应同步给分．

（22）解：（Ⅰ）∵，            ……2分

∵，

∴时，递增，时，递减，时，递增，

所以的极大值点为，极小值点为，                     ……4分

而，，，              ……5分

（的图像如右图，供评卷老师参考）

所以，的最小值是．                                      ……6分

（II）由（Ⅰ）知在的值域是：

当时，为，当时，为．                ……8分                 

而在的值域是为，             ……9分

所以，当时，令，并解得，

当时，令，无解．

因此，的取值范围是．                                     ……12分

注：学生使用其它解法应同步给分．