题目列表(包括答案和解析)
C．选修4-4：坐标系与参数方程
在极坐标系下，已知圆O：
和直线
，
（1）求圆O和直线
的直角坐标方程；（2）当
时，求直线与圆O公共点的一个极坐标.
D．选修4-5：不等式证明选讲
对于任意实数
和
，不等式
恒成立，试求实数
的取值范围．
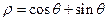和直线
，
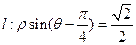的直角坐标方程；（2）当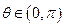
时，求直线与圆O公共点的一个极坐标.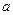
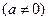和
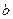，不等式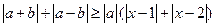
恒成立，试求实数
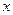的取值范围．C
[解析] 由基本不等式，得ab≤
＝
＝
－ab，所以ab≤
，故B错；
＋
＝
＝
≥4，故A错；由基本不等式得
≤
＝
，即
＋
≤
，故C正确；a2＋b2＝(a＋b)2－2ab＝1－2ab≥1－2×＝，故D错．故选C.
．定义域为R的函数
满足
，且当
时，
，则当
时，
的最小值为（ ）
（A）
（B）
（C）
（D）
．过点
作圆
的弦，其中弦长为整数的共有 （ ）
A.16条 B. 17条 C. 32条 D. 34条
17．本题满分14分．已知函数
。
（1）
求函数
在
上的值域；
（2）
在
中，若
，求
的值。
16 
21．本小题满分12分．
已知函数fx．=lnx-
，
（I） 求函数fx．的单调增区间；
（II）
若函数fx．在[1，e]上的最小值为
，求实数a的值。
3.已知
，则
的值为 ．
A.－2 B.－1 C.1 D.2
19．解：1．∵
，
，
∴
，
∵
，
∴
，
即
，
.
2．∵
，
，∴
，
∵，∴
，
∵
，∴
，
∴
，
.
20．此题主要考查数列．等差．等比数列的概念．数列的递推公式．数列前n项和的求法
同时考查学生的分析问题与解决问题的能力，逻辑推理能力及运算能力．
解：I．
Ⅱ．
16．本题满分14分．
解：1．连
，四边形
菱形 
，
为
的中点， 
又
，
2．当
时，使得
，连
交
于
，交于
，则为 的中点，又为
边上中线，为正三角形
的中心，令菱形的边长为
，则
，
。
即：
。
22．本小题满分14分．
解：I．1．
，
。…………………………………………1分
处取得极值，
…………………………………………………2分
即
………………………………………4分
ii．在
，
由
，
；
当
;
;
.……………………………………6分
面
，
且
又
，
……………9分
Ⅱ．当
，
①
；
②当
时，
，
③
，
从面得
;
综上得，
.………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com