某校对高三年级800名男生的身高(单位：cm)进行了统计，随机抽取的一个容量为50的样本的频率分布直方图的部分图形如图所示，已知第一组与第八组人数相同，第六组、第七组、第八组人数依次构成等差数列．
(1)估计这所学校高三年级全体男生身高180 cm以上(含180 cm)的人数；
(2)求第六组、第七组的频率并补充完整频率分布直方图；
(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生，记他们的身高分别为x、y，求满足|x－y|≤5的事件概率．

查看答案和解析>>

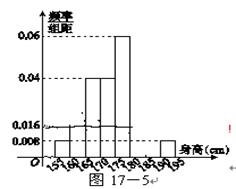
从某学校的800名男生中随机抽取50名测量身高，被测学生身高全部介于155cm和195cm之间，将测量结果按如下方式分成八组：第一组[155，160），第二组[160，165），…，第八组[190，195]，下图是按上述分组方法得到的频率分布直方图的一部分，已知第一组与第八组人数相同，第六组的人数为4人．
（Ⅰ）求第七组的频率；
（Ⅱ）估计该校的800名男生的身高的中位数以及身高在180cm以上（含180cm）的人数；
（Ⅲ）若从身高属于第六组和第八组的所有男生中随机抽取两名男生，求抽出的两名男生是在同一组的概率．

查看答案和解析>>

查看答案和解析>>

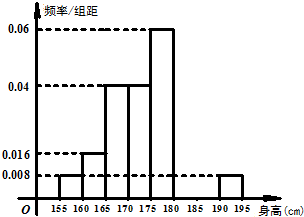
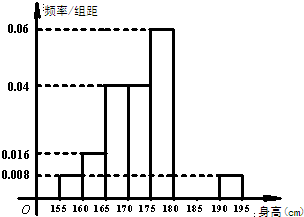从某学校的800名男生中随机抽取50名测量身高，被测学生身高全部介于155cm和195cm之间，将测量结果按如下方式分成八组：第一组[155，160），第二组[160，165），…，第八组[190，195]，右图是按上述分组方法得到的频率分布直方图的一部分，已知第一组与第八组人数相同，第六组的人数为4人．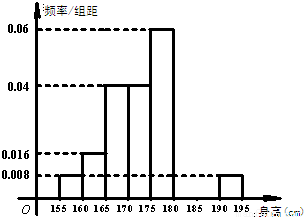
（Ⅰ）求第七组的频率；
（Ⅱ）估计该校的800名男生的身高的中位数以及身高在180cm以上（含180cm）的人数；
（Ⅲ）若从身高属于第六组和第八组的所有男生中随机抽取两名男生，记他们的身高分别为x，y，事件E={|x-y|≤5}，事件F={|x-y|＞15}，求P（E∪F）．

查看答案和解析>>

从某校高二年级名男生中随机抽取名学生测量其身高，据测量被测学生的身高全部在到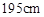之间．将测量结果按如下方式分成组：第一组，第二组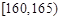， ，第八组，如下右图是按上述分组得到的频率分布直方图的一部分．已知第一组与第八组的人数相同，第六组、第七组和第八组的人数依次成等差数列．
频率分布表如下：

分组	频数	频率	频率/组距

频率分布直方图如下：

（1）求频率分布表中所标字母的值，并补充完成频率分布直方图；
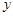（2）若从身高属于第六组和第八组的所有男生中随机抽取名男生，记他们的身高分别为,求满足:的事件的概率．

查看答案和解析>>

17．本题满分14分．已知函数。

（1）       求函数在上的值域；

（2）       在中，若，求的值。

16

21．本小题满分12分．

已知函数fx．=lnx-，

（I）        求函数fx．的单调增区间；

（II）     若函数fx．在[1，e]上的最小值为，求实数a的值。

3.已知，则的值为    ．

A.－2          B.－1        C.1             D.2

19．解：1．∵，，

∴，

∵，

∴，

即，.

2．∵，，∴，

∵，∴，

∵，∴，

∴

，

.

20．此题主要考查数列．等差．等比数列的概念．数列的递推公式．数列前n项和的求法

  同时考查学生的分析问题与解决问题的能力，逻辑推理能力及运算能力．

解：I．

Ⅱ．

16．本题满分14分．

解：1．连，四边形菱形   ，

  为的中点，

又

               ，

2．当时，使得，连交于，交于，则为 的中点，又为边上中线，为正三角形的中心，令菱形的边长为，则，。

   即：   。

22．本小题满分14分．

解：I．1．，

    。…………………………………………1分

    处取得极值，

    …………………………………………………2分

    即

    ………………………………………4分

   ii．在，

    由

           ，

    ；

    当;

    ;

    .……………………………………6分

    面

    ，

    且

    又

    ，

    ……………9分

   Ⅱ．当，

    ①；

    ②当时，

    ，

    ③，

    从面得;

    综上得，.………………………14分