
题目列表(包括答案和解析)
(本小题满分12分)
(方案一)已知: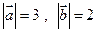 ,
, 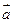 与
与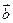 的夹角为
的夹角为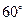 ,
,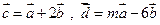 (
(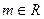 ) 当m为何值时,
) 当m为何值时,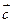 与
与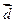 垂直?
垂直?
(本小题满分12分)
某市举行一次数学新课程骨干培训,共邀请15名使用不同版本教材的教师,数据如下表所示:
|
版本 |
人教A版 |
人教B版 |
||
|
性别 |
男教师 |
女教师 |
男教师 |
女教师 |
|
人数 |
6 |
3 |
4 |
2 |
(1)从这15名教师中随机选出2名,则2人恰好是教不同版本的男教师的概率是多少?
(2)培训活动随机选出2名代表发言,设发言代表中使用人教B版的女教师人数为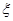 ,求随机变量
,求随机变量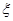 的分布列和数学期望
的分布列和数学期望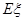 .
.
(本小题满分12分)
如图一所示,边长为1的正方体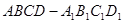 中,
中, 分别为
分别为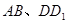 的中点。
的中点。
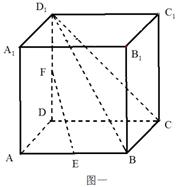
(Ⅰ)证明: ;
;
(Ⅱ)若 为
为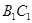 的中点,证明:
的中点,证明: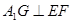 ;
;
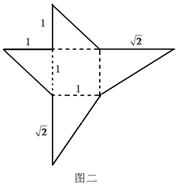
(Ⅲ)如图二所示为一几何体的展开图,沿着图中虚线将它们折叠起来,所得几何体的体积为 ,若正方体
,若正方体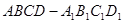 的体积为
的体积为 ,求
,求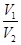 的值。
的值。
(本小题满分12分)
某人向一目射击4次,每次击中目标的概率为![]() 。该目标分为3个不同的部分,第一、二、三部分面积之比为1:3:6。击中目标时,击中任何一部分的概率与其面积成正比。
。该目标分为3个不同的部分,第一、二、三部分面积之比为1:3:6。击中目标时,击中任何一部分的概率与其面积成正比。
(Ⅰ)设X表示目标被击中的次数,求X的分布列;
(Ⅱ)若目标被击中2次,A表示事件“第一部分至少被击中1次或第二部分被击中2次”,求P(A) ![]()
![]()
本小题满分12分)
今有一长2米宽1米的矩形铁皮,如图,在四个角上分别截去一个边长为x米的正方形后,沿虚线折起可做成一个无盖的长方体形水箱(接口连接问题不考虑).
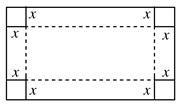
(Ⅰ)求水箱容积的表达式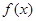 ,并指出函数
,并指出函数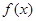 的定义域;
的定义域;
(Ⅱ)若要使水箱容积不大于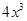 立方米的同时,又使得底面积最大,求x的值.
立方米的同时,又使得底面积最大,求x的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com