
题目列表(包括答案和解析)
(08年扬州中学) (16分)
用![]() 表示数列
表示数列![]() 从第
从第![]() 项到第
项到第![]() 项(共
项(共![]() 项)之和.
项)之和.
(1)在递增数列![]() 中,
中,![]() 与
与![]() 是关于
是关于![]() 的方程
的方程![]() (
(![]() 为正整数)的两个根.求
为正整数)的两个根.求![]() 的通项公式并证明
的通项公式并证明![]() 是等差数列;
是等差数列;
(2)对(1)中的数列![]() ,判断数列
,判断数列![]() ,
,![]() ,
,![]() ,…,
,…,![]() 的类型;
的类型;
(3)对一般的首项为![]() ,公差为
,公差为![]() 的等差数列,提出与(2)类似的问题,你可以得到怎样的结论,证明你的结论.
的等差数列,提出与(2)类似的问题,你可以得到怎样的结论,证明你的结论.
已知函数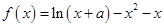 在
在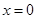 处取得极值.
处取得极值.
(1)求实数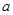 的值;
的值;
(2)若关于 的方程
的方程 在区间
在区间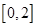 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数 的取值范围;
的取值范围;
(3)证明:对任意的正整数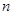 ,不等式
,不等式 都成立.
都成立.
已知函数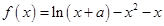 在
在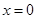 处取得极值.
处取得极值.
(1)求实数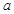 的值;
的值;
(2)若关于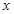 的方程
的方程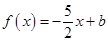 在区间
在区间 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数 的取值范围;
的取值范围;
(3)证明:对任意的正整数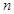 ,不等式
,不等式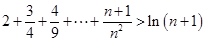 都成立.
都成立.
(本小题满分14分)已知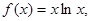
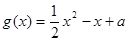 .(1)当
.(1)当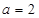 时,求
时,求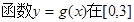 上的值域;
(2) 求函数
上的值域;
(2) 求函数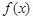 在
在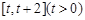 上的最小值;(3) 证明: 对一切
上的最小值;(3) 证明: 对一切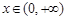 ,都有
,都有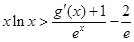 成立
成立
一、填空题:
1.  2. 三 3. 1 4. 25 5.
2. 三 3. 1 4. 25 5.  6. -1 7.
6. -1 7.  8. (1,0)
8. (1,0)
9.  10. 8 11. 1 12. (0,2) 13. 2026 14. ①②③
10. 8 11. 1 12. (0,2) 13. 2026 14. ①②③
二、解答题:
15. 解:(1)因为 ,
, ,所以
,所以
 …………………………4分
…………………………4分
 ……………………………………………………..6分
……………………………………………………..6分
因此,当 ,即
,即 (
( )时,
)时, 取得最大值
取得最大值 ;…8分
;…8分
(2)由 及
及 得
得 ,两边平方得
,两边平方得
 ,即
,即 .……………………………………………12分
.……………………………………………12分
因此, .……………………………14分
.……………………………14分
16.解:由已知不等式得
 ①
①
或  ②
②
不等式①的解为

不等式②的解为 或
或
 …………………………………………………4分
…………………………………………………4分
因为,对 或
或 或
或 时,P是正确的
时,P是正确的 ………………………..6分
………………………..6分
对函数 求导
求导 …8分
…8分
令 ,即
,即

当且仅当D>0时,函数f( )在(-¥,+¥)上有极值
)在(-¥,+¥)上有极值
由 得
得 或
或 ,
,
因为,当 或
或 时,Q是正确的
时,Q是正确的 ………………………………………………12分
………………………………………………12分
综上,使P正确且Q正确时,实数m的取值范围为(-¥,-1)È
 ……….14分
……….14分
17.解:(1)因为函数 的图象关于原点对称,所以
的图象关于原点对称,所以 即
即 ,
,
 ,得
,得 或
或 ……………………………………….2分
……………………………………….2分
当 时,
时, 舍去;
舍去;
当 时,
时, ,令
,令 ,解得
,解得 或
或 .
.
所以符合条件的m值为-1 …………………………………………………………………4分
(2)由(1)得 ,任取
,任取 ,
,

 ……………………6分
……………………6分
 ∴
∴ ,
,
∴ ………………………………………………………………….8分
………………………………………………………………….8分
∴当 时,
时, 即
即 ,此时
,此时 为增函数;
为增函数;
当 时,
时, 即
即 ,此时
,此时 为减函数…10分
为减函数…10分
(3)由(2)知,当 时
时 在
在 上为减函数;同理在
上为减函数;同理在 上也为减函数
上也为减函数
当 时,
时, 与已知矛盾,舍去;………………12分
与已知矛盾,舍去;………………12分
当 时,因为函数
时,因为函数 的值域为
的值域为
∴ 且
且 ,解得
,解得 ,
, ……………………………………14分
……………………………………14分
18.解:(1)由 ,令
,令 ,则
,则 ,又
,又 ,所以
,所以 .
.
 ,则
,则 . …………………………………………………………………………………….2分
. …………………………………………………………………………………….2分
当 时,由
时,由 ,可得
,可得 . 即
. 即 ..6分
..6分
所以 是以
是以 为首项,
为首项, 为公比的等比数列,于是
为公比的等比数列,于是 . ……8分
. ……8分
(2)数列 为等差数列,公差
为等差数列,公差 ,可得
,可得 . ….10分
. ….10分
从而 . ……………………………………………..12分
. ……………………………………………..12分
∴
 ……….16分
……….16分
19.解:(1)依题意知汽车从甲地匀速行驶到乙地所用时间为 ,全程运输成本为
,全程运输成本为 ……………………………………….4分
……………………………………….4分
故所求函数及其定义域为 ………………………….6分
………………………….6分
(2)依题意知a,v都为正数,故有
当且仅当 .即
.即 时上式中等号成立………………………...8分
时上式中等号成立………………………...8分
(1)若 ,即
,即 时则当
时则当 时,全程运输成本y最小.10分
时,全程运输成本y最小.10分
(2)若 ,即
,即 时,则当
时,则当 时,有
时,有

 .
.
 。也即当v=100时,全程运输成本y最小.…….14分
。也即当v=100时,全程运输成本y最小.…….14分
综上知,为使全程运输成本y最小,当 时行驶速度应为
时行驶速度应为 千米/时;
千米/时;
当 时行驶速度应为v=
时行驶速度应为v=
20.解: (1)  ,当
,当 ,
, ,
, 单调递减,当
单调递减,当 ,
, ,
, 单调递增.………………………………………………………………..2分
单调递增.………………………………………………………………..2分
①  ,t无解;
,t无解;
②  ,即
,即 时,
时, ;
;
③  ,即
,即 时,
时, 在
在 上单调递增,
上单调递增, ;
;
所以 .…………………………………………………………..6分
.…………………………………………………………..6分
(2)  ,则
,则 ,………………………………………..8分
,………………………………………..8分
设 ,则
,则 ,
, ,
, ,
, 单调递减,
单调递减, ,
, ,
, 单调递增,所以
单调递增,所以 ……………………….10分
……………………….10分
因为对一切 ,
, 恒成立,所以
恒成立,所以 ;………………..12分
;………………..12分
(3) 问题等价于证明 ,由⑴可知
,由⑴可知 的最小值是
的最小值是 ,当且仅当
,当且仅当 时取到………………………………………………………….14分
时取到………………………………………………………….14分
设 ,则
,则 ,易得
,易得 ,当且仅当
,当且仅当 时取到,从而对一切
时取到,从而对一切 ,都有
,都有 成立.……………………………..16分
成立.……………………………..16分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com