查看答案和解析>>

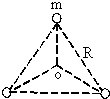宇宙间存在一些离其它恒星较远的三星系统．其中有一种三星系统如图所示，三颗质量相等的星位于等边三角形的三个顶点上，任意两颗星的距离均为R，并绕其中心O做匀速圆周运动．如果忽略其它星体对它们的引力作用，引力常数为G．以下对该三星系统的说法中正确的是（　　）

A、每颗星做圆周运动的半径为等边三角形的边长R

B、每颗星做圆周运动的加速度与三星的质量无关

C、每颗星做圆周运动的周期为T=2πR R 3Gm

D、每颗星做圆周运动的线速度为v= Gm R

查看答案和解析>>

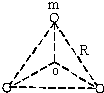宇宙间存在一些离其它恒星较远的三星系统．其中有一种三星系统如图所示，三颗质量相等的星位于等边三角形的三个顶点上，任意两颗星的距离均为R，并绕其中心O做匀速圆周运动．如果忽略其它星体对它们的引力作用，引力常数为G．以下对该三星系统的说法中正确的是（　　）

A、每颗星做圆周运动的半径为等边三角形的边长R

B、每颗星做圆周运动的加速度与三星的质量无关

C、利用所给物理量不能求出每颗星做圆周运动的线速度大小

D、利用所给物理量能求出每颗星做圆周运动的周期

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

一、二选择题：1-5题为单选题，每小题只有一个选项符合题意，选对的得3分，错选或不答的得0分，每小题3分，共15分；6-9小题为多选题，每小题有多个选项符合题意，全部选对的得4分，选对但不全的得2分，错选或不答的得0分，每小题4分，共16分。

题号

1

2

3

4

5

6

7

8

9

答案

C

A

B

B

D

AD

ACD

CD

AC

三．简答题：本题共4小题，共42分

10：⑴C                                                 3分

⑵ A     a＝4.0×10⁵m/s²          各2分，计4分

11. （1）S₁闭合，S₂断开

        电炉中的电流                                 2分

         E=I?(R+r）=120V                                       2分

   （2）S₁ S₂均合上，电炉的功率为P

        电炉中的电流                         2分

        外电压U=95V

              总电流

        ∴I_A=I?I_R=20A                                          3分

        电解槽内阻消耗的功率=200W                    3分

12.(1)在6.122～6.125范围内均可     10.50        各2分，计4分

(2)0.25m/s     0.30m/s²                      各2分，计4分

13．（1）BC                                                          3分

（2）AC                                                          3分

（3）2.0     1.50              1.0                        各2分，计6分

（4）不能                                                          1分

当电流表读数达到0.6A时，从图乙中可以看出测路端电压的电压表V₁的读数会小于V₂的读数，在电路里是不可能实现的．（或者电路中的最大电流应该是0.5A）         2分

四．计算题：本题共3小题，共47分

14．（1）微粒在加速电场中应用动能定理得

                                                            2分

代入数据解得v₀=1.0×10⁴m/s                                 　           2分

（2）微粒在偏转电场中做类平抛运动，则有

                                                             1分

                                                         1分

飞出电场时，速度偏转角的正切为

       解得  θ=30^o                                    2分

（3）微粒进入磁场后在洛仑兹力作用下做匀速圆周运动，如图所示，由向心力公式有

                              2分

又因为                             2分

解得                     1分

由图示几何关系知=120°，所以微粒在磁场中运动的时间为                       2分

15．（1）电荷做类平抛运动，则有

a =                               1分

Rsinθ= v₀t                             1分

R+Rcosθ=at²                                     1分

由以上三式得         2分

（2）由（1）中的结论可得粒子从A点出发时的动能为

                             2分

则经过P点时的动能为

E_k=Eq(R+Rcosθ)＋m v₀² = EqR (5+3cosθ)               3分

(3)从上式可以看出，当θ从120°变化到60°的过程中，接收屏上电荷的动能逐渐增大，因此D点接收到的电荷的末动能最大．                                                2分

最大动能为：E_kD=Eq(R+Rcos60°)＋m v₀² = EqR (5+3cos60°) = EqR       3分

16．（1）解除锁定弹开物块AB后，两物体的速度大小

                                            2分

弹簧储存的弹性势能                                1分

（2）物块B滑上传送带匀减速运动，当速度减为零时，滑动的距离最远．

由动能定理得：                                       2分

得：                                                      1分

（3）物块B沿传送带向左返回时，先匀加速运动，物块速度与传送带速度相同时再一起匀速运动，设物块B加速到传送带速度v需要滑动的距离为

由   　     得                           2分

表明物块B滑回水平面MN的速度没有达到传送带的速度

所以:                                               1分

（4）设弹射装置对物块A做功为，则：                 1分

AB碰后速度互换，B的速度  =                                      1分

B要刚好能滑出传送带的Q端，由能量关系有：                1分

又m_A=m_B，  联立解得：                            1分

                                                           1分

在B滑过传送带的过程中，传送带移动的距离：   1分

因摩擦产生的内能为：            2分