
题目列表(包括答案和解析)
已知椭圆![]() 的离心率为
的离心率为![]() ,短轴的一个端点到右焦点的距离为2,
,短轴的一个端点到右焦点的距离为2,
(1)试求椭圆M的方程;
(2)若斜率为![]() 的直线l与椭圆M交于C、D两点,点P(1,
的直线l与椭圆M交于C、D两点,点P(1,![]() )为椭圆M上一点,记直线PC的斜率为k1,直线PD的斜率为k2,试问:k1+k2是否为定值?请证明你的结论.
)为椭圆M上一点,记直线PC的斜率为k1,直线PD的斜率为k2,试问:k1+k2是否为定值?请证明你的结论.
(本题满分14分)
已知椭圆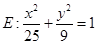 ,直线
,直线 ,F为椭圆
,F为椭圆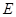 的右焦点,M为椭圆
的右焦点,M为椭圆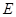 上任意一点,记M到直线L的距离为d.
上任意一点,记M到直线L的距离为d.
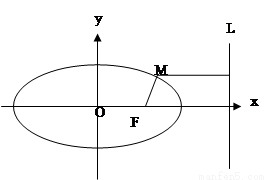
(Ⅰ) 求证: 为定值;
为定值;
(Ⅱ) 设过右焦点F的直线m的倾斜角为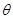 ,m交椭圆
,m交椭圆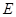 于A、B两点,且
于A、B两点,且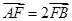 ,求
,求 的值。
的值。
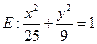 ,直线
,直线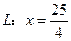 ,F为椭圆
,F为椭圆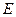 的右焦点,M为椭圆
的右焦点,M为椭圆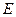 上任意一点,记M到直线L的距离为d.
上任意一点,记M到直线L的距离为d.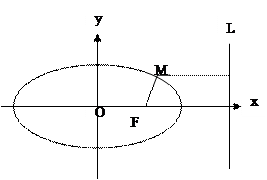
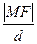 为定值;
为定值;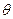 ,m交椭圆
,m交椭圆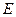 于A、B两点,且
于A、B两点,且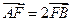 ,求
,求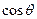 的值。
的值。如图,圆O与离心率为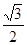 的椭圆T:
的椭圆T: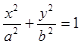 (
(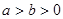 )相切于点M
)相切于点M 。
。
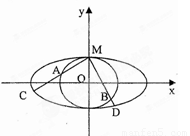
⑴求椭圆T与圆O的方程;
⑵过点M引两条互相垂直的两直线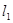 、
、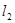 与两曲线分别交于点A、C与点B、D(均不重合)。
与两曲线分别交于点A、C与点B、D(均不重合)。
①若P为椭圆上任一点,记点P到两直线的距离分别为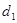 、
、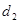 ,求
,求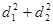 的最大值;
的最大值;
②若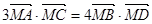 ,求
,求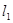 与
与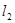 的方程。
的方程。
如图,圆O与离心率为 的椭圆T:
的椭圆T: (
( )相切于点M
)相切于点M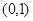 。
。
⑴求椭圆T与圆O的方程;
⑵过点M引两条互相垂直的两直线 、
、 与两曲线分别交于点A、C与点B、D(均不重合)。
与两曲线分别交于点A、C与点B、D(均不重合)。
①若P为椭圆上任一点,记点P到两直线的距离分别为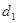 、
、 ,求
,求 的最大值;
的最大值;
②若 ,求
,求 与
与 的方程。
的方程。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com