
题目列表(包括答案和解析)
| 2 | x |
| 1 |
| 2 |
| 3π |
| 4 |
| AB |
| BC |
| x2 |
| 4 |
| y2 |
| m |
| 4 |
| 3 |
给出下列四个结论:
①若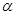 、
、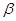 为锐角,
为锐角,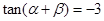 ,
,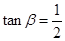 ,则
,则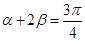 ;
;
②在△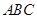 中,若
中,若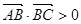 ,则△
,则△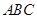 一定是钝角三角形;
一定是钝角三角形;
③已知双曲线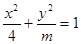 ,其离心率
,其离心率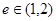 ,则m的取值范围是(-12,0);
,则m的取值范围是(-12,0);
④当a为任意实数时,直线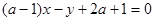 恒过定点
恒过定点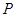 ,则焦点在y轴上且过点
,则焦点在y轴上且过点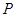 的抛物线的标准方程是
的抛物线的标准方程是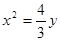 .其中所有正确结论的个数是
.其中所有正确结论的个数是
A .1 B.2 C.3 D.4
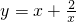 在区间[2,+∞)上单调递增;
在区间[2,+∞)上单调递增;①若A、B、C、D是平面内四点,则必有![]() +
+![]() =
=![]() +
+![]() ;
;
②“a>b>0”是“ab<![]() ”的充要条件;
”的充要条件;
③如果函数f(x)对任意的x∈R都满足f(x)=-f(2+x),则函数f(x)是周期函数;
④已知Sn是等差数列{an}(n∈N+)的前n项和,且S6>S7>S5,则S12>0.
其中正确结论的序号是___________.(填上所有正确结论的序号)
一、选择题:本大题共12小题,每小题5分,共60分.
1. D 2. D 3. D 4. C 5. A
6. D提示: 用 代换x得:
代换x得: 
 ,
,
解得: ,而
,而 单调递增且大于等于0,
单调递增且大于等于0, ,选D。
,选D。
7. B 8. C 9. B
10.B提示: ,若函数在
,若函数在 上有大于零的极值点,即
上有大于零的极值点,即 有正根。当有
有正根。当有 成立时,显然有
成立时,显然有 ,此时
,此时 ,由
,由 得到参数
得到参数 的范围为
的范围为 。
。
11. D提示:由奇函数 可知
可知 ,而
,而 ,
,
则 ,当
,当 时,
时, ;当
;当 时,
时, ,
,
又 在
在 上为增函数,则奇函数
上为增函数,则奇函数 在
在 上为增函数,
上为增函数, .
.
12. D
二、填空题:本大题共4个小题,每小题4分,共16分.
13.  14. 1-cos1 15.
14. 1-cos1 15.
 16.②③
16.②③
三、解答题:本大题共6小题,共74分.
17.(本小题满分12分)
解(Ⅰ)由题意可设二次函数f(x)=a(x-1)(x-3)(a<0) ………2分
当x=0时,y=-3,即有-3=a(-1)(-3),
解得a=-1,
f(x)= -(x-1)(x-3)= ,
,
 的解析式为
的解析式为 =
= . ……………………6分
. ……………………6分
(Ⅱ)y=f(sinx)=
= .
……………………8分
.
……………………8分
 ,
,
 ,
,
则当sinx=0时,y有最小值-3;
当sinx=1时,y有最大值0. …………………12分
18.(本小题满分12分)
解: (Ⅰ)改进工艺后,每件产品的销售价为 ,月平均销售量为
,月平均销售量为 件,则月平均利润
件,则月平均利润 (元),
(元),
∴ 与
与 的函数关系式为
的函数关系式为
 .…………6分
.…………6分
(Ⅱ)由 得
得 ,
, (舍), ……………8分
(舍), ……………8分
当 时
时 ;
; 时
时 ,
,
∴函数
 在
在 取得最大值.
取得最大值.
故改进工艺后,产品的销售价为
 元时,旅游部门销售该纪念品的月平均利润最大.
……………………12分
元时,旅游部门销售该纪念品的月平均利润最大.
……………………12分
19.(本小题满分12分)
解:(Ⅰ)设函数 图象上任意一点
图象上任意一点 关于原点的对称点为
关于原点的对称点为 ,则
,则
 ……………………4分
……………………4分
由题知点 在函数
在函数 的图象上,
的图象上,
∴ . ……………………6分
. ……………………6分
(Ⅱ)由
当 时,
时, ,此时不等式无解
,此时不等式无解
当 时,
时, ,解得
,解得

因此,原不等式的解集为
 …………………………12分
…………………………12分
20.(本小题满分12分)
解:设公司在甲电视台和乙电视台做广告的时间分别为 分钟和
分钟和 分钟,总收益为
分钟,总收益为 元,由题意得
元,由题意得  ………………………………3分
………………………………3分
 目标函数为
目标函数为 .………5分
.………5分
二元一次不等式组等价于
作出二元一次不等式组所表示的平面区域,即可行域. ………………8分
如图:作直线 ,
,
即 .
.
平移直线 ,从图中可知,当直线
,从图中可知,当直线 过
过 点时,目标函数取得最大值.
点时,目标函数取得最大值.
联立 解得
解得 .
.
 点
点 的坐标为
的坐标为 .
………………………10分
.
………………………10分
 (元)
(元)
答:该公司在甲电视台做100分钟广告,在乙电视台做200分钟广告,公司的收益最大,最大收益是70万元. …………………………12分
21.(本小题满分12分)
解:由 得
得 ,
,
又 ,所以
,所以 ,
,
当 时,1<
时,1< ,即
,即 为真时实数
为真时实数 的取值范围是1<
的取值范围是1< . …………2分
. …………2分
由 ,得
,得 ,即
,即 为真时实数
为真时实数 的取值范围是
的取值范围是 . ……4分
. ……4分
若 为真,则
为真,则 真且
真且 真,
真,
所以实数 的取值范围是
的取值范围是 .
……………………6分
.
……………………6分
(Ⅱ)
 是
是 的充分不必要条件,即
的充分不必要条件,即

 ,且
,且

 , ……………8分
, ……………8分
设A= ,B=
,B= ,则
,则

 ,
,
又A= =
= , B=
, B= =
= }, ……………10分
}, ……………10分
则0< ,且
,且
所以实数 的取值范围是
的取值范围是 . ……………………12分
. ……………………12分
22.(本小题满分14分)
解:(Ⅰ)因为 ,
,
所以 ,
,
因此 .
………………………………4分
.
………………………………4分
(Ⅱ)由(Ⅰ)知,
 ,
,
 .
………………5分
.
………………5分
当 时,
时, , ………………6分
, ………………6分
当 时,
时, .
………………7分
.
………………7分
所以 的单调增区间是
的单调增区间是 ,
,
 的单调减区间是
的单调减区间是 .
………………8分
.
………………8分
(Ⅲ)由(Ⅱ)知, 在
在 内单调增加,在
内单调增加,在 内单调减少,在
内单调减少,在 上单调增加,且当
上单调增加,且当 或
或 时,
时, ,
………………9分
,
………………9分
所以 的极大值为
的极大值为 ,极小值为
,极小值为 . ……10分
. ……10分
因此 ,
,
 ,
………………12分
,
………………12分
所以在 的三个单调区间
的三个单调区间 直线
直线 有
有 的图象各有一个交点,当且仅当
的图象各有一个交点,当且仅当 ,
,
因此, 的取值范围为
的取值范围为 .
………………14分
.
………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com