设m,n是整数，则“m,n均为偶数”是“m+n是偶数”的【　  】.

A .充分而不必要条件                       B .必要而不充分条件             

C .充要条件                                       D .既不充分也不必要条件

【解析】本小题考查直线方程的求法。画草图，由对称性可猜想。

事实上，由截距式可得直线，直线，两式相减得，显然直线AB与CP的交点F满足此方程，又原点O也满足此方程，故为所求的直线OF的方程。

答案。

【解析】。由题得  所以不等式的解集为。

用数学归纳法证明：

．

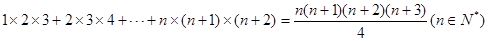【解析】首先证明当n=1时等式成立，再假设n=k时等式成立，得到等式

，

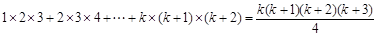下面证明当n=k+1时等式左边

，

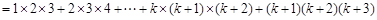根据前面的假设化简即可得到结果，最后得到结论．

【解析】B.由题得三视图对应的直观图是如图所示的直四棱柱，

。所以选B