题目列表(包括答案和解析)
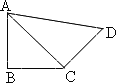
如图，在平面四边形ABCD中，AB＝BC＝CD＝a，∠ABC＝90°，∠BCD＝135°，沿对角线AC将此四边形折成直二面角
1）求证：AB⊥平面BCD
2）求三棱锥D－ABC的体积
3）求点C到平面ABD的距离
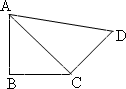
如图，在平面四边形ABCD中，AB＝BC＝CD＝a，∠ABC＝90°，∠BCD＝135°，沿对角线AC将此四边形折成直二面角
(1)求证：AB⊥平面BCD
(2)求三棱锥D－ABC的体积
(3)求点C到平面ABD的距离
如图，在平面四边形ABCD中，AB＝BC＝CD＝a，∠ABC＝90°，∠BCD＝135°，沿对角线AC将此四边形折成直二面角
1)求证：AB⊥平面BCD
2)求三棱锥D－ABC的体积
3)求点C到平面ABD的距离
在三棱锥D－ABC中，AC＝BC＝CD＝2，CD⊥平面BCD，∠ACB＝90°．若其主视图，俯视图如图所示，则其左视图的面积为
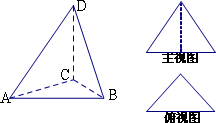
2
如图1，∠ACB＝45°，BC＝3，过动点A作AD⊥BC，垂足D在线段BC上且异于点B，连接AB，沿AD将△ABD折起，使∠BDC＝90(如图2所示)．
(Ⅰ)当BD的长为多少时，三棱锥A－BCD的体积最大；
(Ⅱ)当三棱锥A＝BCD的体积最大时，设点E，M分别为棱BC，AC的中点，试在棱CD上确定一点N，使得EN⊥BM，并求EN与平面BMN所成角的大小．
一、选择题（每题5分，共60分）：
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
理D
文A
B
D
D
B
A
B
A
C
理D
文A
D
A
二、填空题（每题4分，共16分）：
13．1 14．
15．
； 16． 24。
三、解答题（本大题共6小题，共74分）：
17解：sin3x=sin(2x+x)=sin2xcosx+cos2xsinx=2sinxcos
x+(1-2sinx)sinx=3sinx-4sinx
∴f(x)=3-4sinx+2sin2x=3-2(1-cos2x)+2sin2x
=1+2
sin(2x+
)（x≠kπ k∈Z) ……(6分）
（１）f(x)的周期T=
………………（8分）
（２）当sin(2x+)= -1
x= 
+kπ (k∈Z)时，f(x)
=1-2…………（10分）
此时x的集合为{x|x= +kπ，k∈Z）………………（12分）
18、解：（１）P=1－
＝
……（4分）
（２）要使
值为整数 当a=1时，（a,b)=(1,1),(1,2),(1,4)
当a=2时，（a,b)=(2,1),(2,4) 当a=3时，（a,b)=(3,1),(3,6)
a=4,5,6时，（a,b)分别为（4,1）（5,１）（6,１） 共10种 ……（10分）
故所求概率为P=
=
……………………（12分）
19、（１）当λ＝
时，面BEF⊥面ACD
…（2分）
证明如下：
=
= 
EF∥CD
CD⊥面ABC ,又CD∥EF
∴
面BEF⊥面ACB
……………
（6分）
（２）作EO⊥CF于O，连BO
∵
BE⊥面EFC
∴EO为BO在面EFC内射影∴BO⊥CF
∴∠EOB为二面角E－CF－B的平面角…………（8分）
在RtΔEFC中EO?CF＝EC?EF
EO?
=
?
EO=
在Rt△BOE中，BE=
EO=………………（10分）
∴
∠EOB=
=
∴ ∠EOB=60°故二面角E-CF-B的大小为60°（12分）
20、解（１）f
'(x)=
+x (x>0)
若a≥0，则f ' (x)>0 f(x)在（0,＋∞）递增………（2分）
若a<0，令f ' (x)=0 x =±
f ' (x)=
>0, 又x>0x∈(，+∞）
f ' (x)<0 x∈(0，）
∴f(x)的递增区间为（，+∞），递减区间为（0,）……（6分）
（２）令φ(x)=f(x)-g(x)= lnx+
+
(x>0)
则φ ' (x)= 
+x
=
=
令φ ' (x)=0 x=1………………………………（8分）
当0<x<1时，φ ' (x)>0φ (x)递增 当x>1时，φ ' (x)<0 φ (x)递减
∴x=1时φ (x)
=-
+=0……………………（10分）
∴φ (x)≤0 即f (x)≤g(x) ∴a=1时的f(x)图象不在g(x)图象上方………（12分）
22．解：（(1) 可设
, 得
= tan
=
= 
(2) 设
, 得直线
的方程为
方程 
= -
所以
所以有
由
得
所以
=(
(3) 证明：当
时,
左边=
=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com