在本次数学期中考试试卷中共有10道选择题，每道选择题有4个选项，其中只有一个是正确的。评分标准规定：“每题只选一项，答对得5分，不答或答错得0分”.某考生每道题都给出一个答案, 且已确定有7道题的答案是正确的，而其余题中，有1道题可判断出两个选项是错误的，有一道可以判断出一个选项是错误的，还有一道因不了解题意只能乱猜。试求出该考生：

（1）选择题得满分(50分)的概率；

（2）选择题所得分数的数学期望。

【解析】第一问总利用独立事件的概率乘法公式得分为50分，10道题必须全做对．在其余的3道题中，有1道题答对的概率为，有1道题答对的概率为，还有1道答对的概率为，

所以得分为50分的概率为：

第二问中，依题意，该考生得分的范围为｛35，40，45，50｝         

得分为35分表示只做对了7道题，其余各题都做错，

所以概率为                            

得分为40分的概率为： 

同理求得，得分为45分的概率为： 

得分为50分的概率为：

得到分布列和期望值。

解：（1）得分为50分，10道题必须全做对．在其余的3道题中，有1道题答对的概率为，有1道题答对的概率为，还有1道答对的概率为，

所以得分为50分的概率为：                   …………5分

（2）依题意，该考生得分的范围为｛35，40，45，50｝            …………6分

得分为35分表示只做对了7道题，其余各题都做错，

所以概率为                              …………7分

得分为40分的概率为：     …………8分

同理求得，得分为45分的概率为：                     …………9分

得分为50分的概率为：                      …………10分

所以得分的分布列为

数学期望

某村计划建造一个室内面积为的矩形蔬菜温室。在温室内，沿左、右两侧与后侧内墙各保留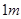宽的通道，沿前侧内墙保留宽的空地，当矩形温室的边长各为多少时，蔬菜的种植面积最大？最大种植面积是多少？

【解析】本试题考查了实际生活中的最值问题的运用，首先确定设矩形温室的长为xm，则宽为800/xm。

依题意有：种植面积：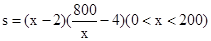

运用导数的思想得到最值。

设矩形温室的长为xm，则宽为800/xm。

依题意有：种植面积：

答：当矩形温室的长为20m，宽为40m时种植面积最大，最大种植面积是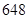m²

（理科）某中学高一年级美术学科开设书法、绘画、雕塑三门校本选修课，学生可选也可不选，学生是否选修哪门课互不影响．已知某学生只选修书法的概率为0.08，只选修书法和绘画的概率是0.12，至少选修一门的概率是0.88．
（1）依题意分别计算该学生选修书法、绘画、雕塑三门校本选修课的概率；
（2）用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积，求随机变量ξ的分布列和数学期望．