
题目列表(包括答案和解析)
袋子中装有大小形状完全相同的m个红球和n个白球,其中m,n满足m>n≥2且m+n≤l0(m,n∈N+),若从中取出2个球,取出的2个球是同色的概率等于取出的2个球是异色的概率.
(Ⅰ) 求m,n的值;
(Ⅱ) 从袋子中任取3个球,设取到红球的个数为 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
【解析】第一问中利用 ,解得m=6,n=3.
,解得m=6,n=3.
第二问中, 的取值为0,1,2,3. P(
的取值为0,1,2,3. P( =0)=
=0)= 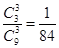 , P(
, P( =1)=
=1)= 
P( =2)=
=2)=  , P(
, P( =3)=
=3)= 
得到分布列和期望值
解:(I)据题意得到 解得m=6,n=3.
解得m=6,n=3.
(II) 的取值为0,1,2,3.
的取值为0,1,2,3.
P( =0)=
=0)= 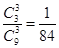 , P(
, P( =1)=
=1)= 
P( =2)=
=2)=  , P(
, P( =3)=
=3)= 
 的分布列为
的分布列为

所以E =2
=2
| x2 |
| a2 |
| y2 |
| b2 |
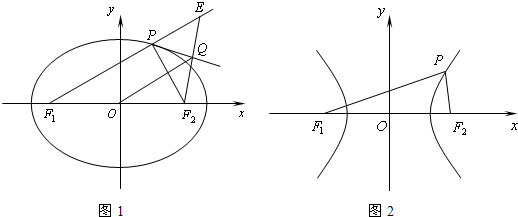
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
设n为正整数,f(n)=1+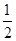 +
+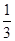 +…+
+…+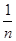 ,计算得f(2)=
,计算得f(2)=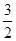 ,f(4)>2,f(8)>
,f(4)>2,f(8)> 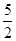 ,f(16)>3,观察上述结果,可推测一般的结论为_________________.
,f(16)>3,观察上述结果,可推测一般的结论为_________________.
设n为正整数,f(n)=1+ +
+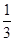 +…+
+…+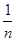 ,计算得f(2)=
,计算得f(2)= ,f(4)>2,f(8)>
,f(4)>2,f(8)>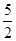 ,f(16)>3,观察上述结果,可推测一般的结论为_______________________________.
,f(16)>3,观察上述结果,可推测一般的结论为_______________________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com