1,3,5
13. 14.
14. =0 15.-
=0 15.- 16.3
16.3
三、解答题
17.解:(1)∵ ……2分
……2分
 …………4分
…………4分
∵ ……6分
……6分
(2)由 ……8分
……8分
∴ ,故tanB=2 …………10分
,故tanB=2 …………10分
18.解:(1)设取出的球不放回袋中,第3次取球才得到红球的概率为P1,
则 ………………6分
………………6分
(2)设取出的球放回袋中,第3次取球才得到红球的概率P2,
则 ………………12分
………………12分
19.(1)证明:∵底面ABCD是菱形,且∠ABC=60°
∴AB=AD=AC=a,在△PAB中,由PA2+AB2=2a=PB2得PA⊥AB,
同理得PA⊥AD, ∴PA⊥平面ABCD
(2)作EG//PA交AD于G,由PA⊥平面ABCD知EG⊥平面ABCD,
作GH//AC于H,连结EH,则EH⊥AC,∴∠EHG为二面角的平面角 ……8分
∵PE:ED=2:1, ∴EG= ,……10分
,……10分
∴ …………12分
…………12分
20.(本小题12分)
解:(Ⅰ)∵ ,
,
∴ 的公比为
的公比为 的等比数列 …………3分
的等比数列 …………3分
又n=1时, ……6分
……6分
(Ⅱ)∵ …………8分
…………8分
∴
 ……
……  ……10分
……10分
以上各式相加得: ]
]
 …………12分
…………12分
21.(本小题12分)
解:(Ⅰ)由题意,设双曲线方程为  ……2分
……2分
又 ,∴方程为
,∴方程为 …4分
…4分
(Ⅱ)由消去y得 ……7分
……7分
当k=2时得 


 ……10分
……10分
当k=-2时同理得

综上:∠MFN为直角. …………12分
22.解:(1) …………2分
…………2分
∵ 上为单调函数,而
上为单调函数,而 不可能恒成立
不可能恒成立
所以 在
在 上恒成立,
上恒成立,
∴ …………6分
…………6分
(2)依题意,方程 有两个不同的实数根
有两个不同的实数根 ,
,
由 ……9分
……9分


所以


所以 
综上: ………………12分
………………12分

 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD= 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD= 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD= 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=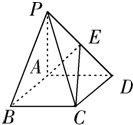 如图,在底面是菱形的四棱锥P-ABCD,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD,∠ABC=60°,PA=AC=a,PB=PD=