
题目列表(包括答案和解析)
求证:①∠BAD=∠CAG;
②AC·AD=AE·AF.
(2)在问题(1)中,当直线l向上平行移动,与⊙O相切时,其他条件不变.
①请你画出变化后的图形,并对照图2-28标记字母;②问题(1)中的两个结论是否成立?如果成立,请证明;如果不成立,请说明理由.

图2-28
(1)求证:AC2=AG·AF.
(2)若E是AD(点A除外)上任意一点,上述结论是否仍然成立?若成立,画出图形,并给予证明;若不成立,请说明理由.
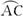
图
(选修4—1几何证明选讲)已知:直线AB过圆心O,交⊙O于AB,直线AF交⊙O于F(不与B重合),直线l与⊙O相切于C,交AB于E,且与AF垂直,垂足为G,连结AC
 求证:(1)
求证:(1)![]() (2)AC2=AE·AF
(2)AC2=AE·AF
23(选修4—4坐标系与参数方程选讲)以直角坐标系的原点O为极点,![]() 轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线
轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线![]() 经过点P(1,1),倾斜角
经过点P(1,1),倾斜角![]() .
.
(I)写出直线![]() 参数方程;
参数方程;
(II)设![]() 与圆
与圆![]() 相交于两点A、B,求点P到A、B两点的距离之积.
相交于两点A、B,求点P到A、B两点的距离之积.
24.选修4-5:不等式选讲
设函数![]() .
.
(Ⅰ)求不等式![]() 的解集;
的解集;
(Ⅱ)![]() ,使
,使![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直线梯形,∠ADC为直角,AD∥BC,AB⊥AC,AC=AB=2,G是△PAC的重心,E为PB中点,F在线段BC上,且CF=2FB.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直线梯形,∠ADC为直角,AD∥BC,AB⊥AC,AC=AB=2,G是△PAC的重心,E为PB中点,F在线段BC上,且CF=2FB.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com