题目列表(包括答案和解析)
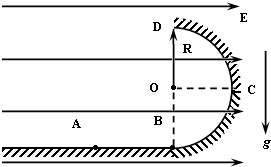如图所示，ABCD为表示竖立放在场强为E=104V/m的水平匀强电场中的绝缘光滑轨道，其中轨道的BCD部分是半径为R的半圆环，轨道的水平部分与半圆环相切A为水平轨道的一点，而且. | AB |
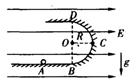如图所示，ABCD为表示竖立放在场强为E=
V/m的水平匀强电场中的绝缘光滑轨道，其中轨道的BCD部分是半径为R的半圆环，轨道的水平部分与半圆环相切，A为水平轨道上的一点，而且AB=R=0. 2 m．把一质量m=100 g、带电q=
C的小球，放在水平轨道的A点处由静止开始释放，在轨道的内侧运动。（
）求：
（1）它到达C点时的速度是多大？
（2）它到达C点时对轨道压力是多大？
（3）小球所能获得的最大动能是多少？[来源:学科网ZXXK]
如图所示，ABCD为表示竖立放在场强E=104v/m的水平匀强电场中的绝缘光滑轨道，其中轨道的BCD部分是半径为R的半圆环，轨道的水平部分与半圆环相切，A为水平轨道的一点，而且
，把一质量m = 100g，带电量q=10－4C的小球放在水平轨道的A点上面由静止开始释放后，在轨道内侧运动（g=10m/s2）求：
（1）它到达C点的速度多大？
（2）它到达C点时对轨道的压力是多大？
（3）小球所能获得的最大的动能是多少？
如图所示，ABCD为表示竖立放在场强为E=104V／m的水平匀强电场中的绝缘光滑轨道,其中轨道的BCD部分是半径为R的半圆环，轨道的水平部分与半圆环相切，A为水平轨道的一点，而且AB=R=0.2m把一质量m=100g、带电q=10-4C的小球，放在水平轨道的A点上面由静止开始被释放后，在轨道的内侧运动。(g取10m／s2)求：
(1)它到达C点时对轨道压力
(2)小球所能获得的最大动能
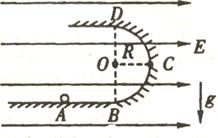
（10分）如图所示，ABCD为表示竖立放在场强为E=104V/m的水平匀强电场中的绝缘光滑轨道，其中轨道的BCD部分是半径为R的半圆环，轨道的水平部分与半圆环相切A为水平轨道的一点，而且AB=R=0.2m把一质量m=100g、带电q=10－4C的小球，放在水平轨道的A点上面由静止开始被释放后，在轨道的内侧运动。（g=10m/s2）求：（1）它到达C点时的速度是多大？
（2）它到达C点时对轨道压力是多大？
（3）小球所能获得的最大动能是多少？
一、单项选择题
1、B 2、A 3、C 4、B 5、A
二、多项选择题
6、ABD 7、BD 8、BCD 9、BD
三、简答题
10、⑴60； ⑵7.18； ⑶3.59
11、（1）0.1s内放电的电量 （2分） （2）5.52×10
（3）6.9×10
12、（1）
实验原理图（图略）：电流表外接法（2分） 滑动变阻器为限流器 （2分）
（2）半导体 （2分）
（3）右 （2分） t=
四、论述计算题
13、（12分）（1）由粒子的飞行轨迹，利用左手定则可知，该粒子带负电荷。
粒子由 A点射入，由
C点飞出，其速度方向改变了 90°，则粒子轨迹半径
1
又 
2
则粒子的比荷 
3
（2）粒子从 D 点飞出磁场速度方向改变了 60°角，故
AD 弧所对圆心角 60°，粒子做圆周运动的半径
4
又
5
所以 
6
粒子在磁场中飞行时间
7
14、（14分）解：（1）、（2）设：小球在C点的速度大小是Vc，对轨道的压力大小为NC，则对于小球由A→C的过程中，应用动能定律列出：
…………………①
在C点的圆轨道径向应用牛顿第二定律，有：
……………………………②
解得：
………③
…………………………④
|
∴小球的最大能动EKM：
………………………………………………⑥
（1分），
（1分）
（1分），
№
（1分）
（1分）， 
。 
（1分），
（1分），
（1分）， 
（1分）。
应将R调至10Ω。
洛仑兹力提供向心力
，由几何关系：
，求出
，垂直纸面向里。 电子做匀速直线运动
， 求出
，沿
轴负方向。
（2）只有电场时，电子从MN上的D点离开电场，如答图2所示，设D点横坐标为
，
， 
，求出D点的横坐标为
，纵坐标为
。
，求出
。