
题目列表(包括答案和解析)
记数列{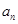 }的前n项和为为
}的前n项和为为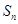 ,且
,且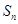 +
+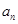 +n=0(n∈N*)恒成立.
+n=0(n∈N*)恒成立.
(1)求证:数列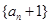 是等比数列;
是等比数列;
(2)已知2是函数f(x)=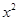 +ax-1的零点,若关于x的不等式f(x)≥
+ax-1的零点,若关于x的不等式f(x)≥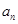 对任意n∈N﹡在x∈(-∞,λ]上恒成立,求实常数λ的取值范围.
对任意n∈N﹡在x∈(-∞,λ]上恒成立,求实常数λ的取值范围.
记数列{ }的前n项和为为
}的前n项和为为 ,且
,且 +
+ +n=0(n∈N*)恒成立.
+n=0(n∈N*)恒成立.
(1)求证:数列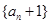 是等比数列;
是等比数列;
(2)已知2是函数f(x)=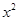 +ax-1的零点,若关于x的不等式f(x)≥
+ax-1的零点,若关于x的不等式f(x)≥ 对任意n∈N﹡在x∈(-∞,λ]上恒成立,求实常数λ的取值范围.
对任意n∈N﹡在x∈(-∞,λ]上恒成立,求实常数λ的取值范围.
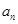 }的前n项和为为
}的前n项和为为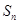 ,且
,且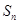 +
+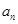 +n=0(n∈N*)恒成立.
+n=0(n∈N*)恒成立.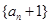 是等比数列;
是等比数列;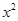 +ax-1的零点,若关于x的不等式f(x)≥
+ax-1的零点,若关于x的不等式f(x)≥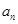 对任意n∈N﹡在x∈(-∞,λ]上恒成立,求实常数λ的取值范围.
对任意n∈N﹡在x∈(-∞,λ]上恒成立,求实常数λ的取值范围.数列 的前n项和记为
的前n项和记为 ,
, ,点
,点 在直线
在直线 上,n∈N*.
上,n∈N*.
(1)求证:数列 是等比数列,并求数列
是等比数列,并求数列 的通项公式
的通项公式 ;
;
(2)设 ,
, 是数列
是数列 的前n项和,求
的前n项和,求 的值.
的值.
数列{ }的前n项和记为
}的前n项和记为 ,a1=t,
,a1=t, =2
=2 +1(n∈N+).
+1(n∈N+).
(Ⅰ)当t为何值时,数列{ }是等比数列;
}是等比数列;
(Ⅱ)在(Ⅰ)的条件下,若等差数列{ }的前n项和
}的前n项和 有最大值,且
有最大值,且 =15,又
=15,又
a1+b1,a2+b2,a3+b3成等比数列,求 .
.
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
答案
B
B
B
C
A
D
B
C
C
B
二、填空题:
题号
11
12
13
14
15
答案
1000
%20数学(文科).files/image225.gif)
%20数学(文科).files/image227.gif)
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
解:(1)由%20数学(文科).files/image121.gif) =
=%20数学(文科).files/image123.gif) ,得:
,得:%20数学(文科).files/image233.gif) =
=%20数学(文科).files/image235.gif) ,
,
即:%20数学(文科).files/image237.gif) ,
,
又∵0<%20数学(文科).files/image117.gif) <
<%20数学(文科).files/image119.gif) ∴
∴%20数学(文科).files/image117.gif) =
=%20数学(文科).files/image240.gif) .
.
(2)直线%20数学(文科).files/image242.gif) 方程为:
方程为:%20数学(文科).files/image244.gif) .
.
%20数学(文科).files/image246.gif) ,
,
点%20数学(文科).files/image029.gif) 到直线
到直线%20数学(文科).files/image242.gif) 的距离为:
的距离为:%20数学(文科).files/image249.gif) .
.
∵%20数学(文科).files/image251.gif)
∴%20数学(文科).files/image253.gif) ∴
∴%20数学(文科).files/image255.gif)
又∵0<%20数学(文科).files/image117.gif) <
<%20数学(文科).files/image119.gif) ,
,
∴sin%20数学(文科).files/image117.gif) >0,cos
>0,cos%20数学(文科).files/image117.gif) <0
<0
∴%20数学(文科).files/image258.gif)
∴sin%20数学(文科).files/image117.gif) -cos
-cos%20数学(文科).files/image117.gif) =
=%20数学(文科).files/image260.gif)
17.(本小题满分12分)
解:(1)%20数学(文科).files/image262.gif)
%20数学(文科).files/image264.gif) 某同学被抽到的概率为
某同学被抽到的概率为%20数学(文科).files/image266.gif)
设有%20数学(文科).files/image192.gif) 名男同学,则
名男同学,则%20数学(文科).files/image269.gif) ,
,%20数学(文科).files/image271.gif)
%20数学(文科).files/image264.gif) 男、女同学的人数分别为
男、女同学的人数分别为%20数学(文科).files/image274.gif)
(2)把%20数学(文科).files/image276.gif) 名男同学和
名男同学和%20数学(文科).files/image137.gif) 名女同学记为
名女同学记为%20数学(文科).files/image279.gif) ,则选取两名同学的基本事件有
,则选取两名同学的基本事件有%20数学(文科).files/image281.gif)
%20数学(文科).files/image283.gif) 共
共%20数学(文科).files/image285.gif) 种,其中有一名女同学的有
种,其中有一名女同学的有%20数学(文科).files/image287.gif) 种
种
%20数学(文科).files/image264.gif) 选出的两名同学中恰有一名女同学的概率为
选出的两名同学中恰有一名女同学的概率为%20数学(文科).files/image290.gif)
(3)%20数学(文科).files/image292.gif) ,
,%20数学(文科).files/image294.gif)
%20数学(文科).files/image296.gif) ,
,%20数学(文科).files/image298.gif)
%20数学(文科).files/image264.gif) 第二同学的实验更稳定
第二同学的实验更稳定
18.(本小题满分14分)
解:(1)%20数学(文科).files/image301.gif) 分别是棱
分别是棱%20数学(文科).files/image303.gif) 中点
中点 %20数学(文科).files/image305.gif)
|