
题目列表(包括答案和解析)
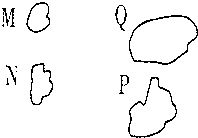 (2011•潍坊二模)如图M,N,P,Q为海上四个小岛,现要建造三座桥,将这四个小岛连接起来,则不同的建桥方法有( )
(2011•潍坊二模)如图M,N,P,Q为海上四个小岛,现要建造三座桥,将这四个小岛连接起来,则不同的建桥方法有( )| 是否愿意提供志愿者服务 性别 |
愿意 | 不愿意 |
| 男生 | 20 | 5 |
| 女生 | 10 | 15 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
(05年湖北卷)某初级中学有学生270人,其中一年级108人,二、三年级各81人,现要利用抽样方法抽取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…,270;使用系统抽样时,将学生统一随机编号1,2,…,270,并将整个编号依次分为10段。如果抽得号码有下列四种情况:
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④30,57,84,111,138,165,192,219,246,270;
关于上述样本的下列结论中,正确的是 ( )
A.②、③都不能为系统抽样 B.②、④都不能为分层抽样
C.①、④都可能为系统抽样 D.①、③都可能为分层抽样
为了了解某市工人开展体育活动的情况,拟采用分层抽样的方法从A,B,C三个区中抽取7个工厂进行调查,已知A,B,C区中分别有18,27,18个工厂
(Ⅰ)从A,B,C区中分别抽取的工厂个数;
(Ⅱ)若从抽取的7个工厂中随机抽取2个进行调查结果的对比,计算这2个工厂中至少有1个来自A区的概率.
【解析】本试题主要考查了统计和概率的综合运用。
第一问工厂总数为18+27+18=63,样本容量与总体中的个体数比为7/63=1/9…3分
所以从A,B,C三个区中应分别抽取的工厂个数为2,3,2。
第二问设A1,A2为在A区中的抽得的2个工厂,B1,B2,B3为在B区中抽得的3个工厂,
C1,C2为在C区中抽得的2个工厂。
这7个工厂中随机的抽取2个,全部的可能结果有1/2*7*6=32种。
随机的抽取的2个工厂至少有一个来自A区的结果有A1,A2),A1,B2),A1,B1),
A1,B3)A1,C2),A1,C1), …………9分
同理A2还能给合5种,一共有11种。
所以所求的概率为p=11/21
|
| a | 2 1 |
| a | 2 1 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com