如题6甲图所示，光滑的水平地面上固定一长为L=1.7m长木板C，板的左端有两小物块A和B，其间夹有一根长为1.0m的轻弹簧，弹簧没有形变，且与物块不相连。已知m_A= m_C=20kg，m_B=40kg，A与木板C、B与木板C的动摩擦因数分别为μ_A=0.50，μ_B=0.25，用水平力F作用于A，让F从零逐渐增大，并使B缓慢地向右移动了0.5m，使弹簧贮存了弹性势能E_O。问：
（1）若弹簧的劲度系数为k=200N/m，以作用力F为纵坐标，A移动的距离为横坐标，试在题6乙的坐标系中作出推力F随A位移的变化图线。
（2）求出弹簧贮存的弹性势能E_O的大小。

查看答案和解析>>

光滑绝缘水平面上固定一个光滑绝缘的斜劈，有一带电小球，质量m=1×10^-9kg，电荷量q=-6.28×10⁸C，小球紧靠在斜劈表面上，如图甲所示．空间充满相互垂直的匀强磁场和匀强电场，磁场方向竖直向下，磁感应强度大小为B=0.1T，电场沿水平方向且与斜劈底边垂直，电场强度大小按图乙所示规律变化，规定图示电场强度的方向为正方向．小球从t=0时刻由静止开始沿D→A方向滑动．已知sinθ=0.1045，cosθ=0.9945（算中取π=3.14，sinθ=0.1，cosθ=1）．求
（1）第1秒末粒子的速度大小
（2）第2秒内粒子离开斜边AD的最大距离
（3）第3秒内粒子能否离开斜劈？若能离开，离开时的速度多大？若不能离开，第3秒末的速度多大？

查看答案和解析>>

光滑绝缘水平面上固定一个光滑绝缘的斜劈，有一带电小球，质量m=1×10^-9kg，电荷量q=-6.28×10⁸C，小球紧靠在斜劈表面上，如图甲所示．空间充满相互垂直的匀强磁场和匀强电场，磁场方向竖直向下，磁感应强度大小为B=0.1T，电场沿水平方向且与斜劈底边垂直，电场强度大小按图乙所示规律变化，规定图示电场强度的方向为正方向．小球从t=0时刻由静止开始沿D→A方向滑动．已知sinθ=0.1045，cosθ=0.9945（算中取π=3.14，sinθ=0.1，cosθ=1）．求
（1）第1秒末粒子的速度大小
（2）第2秒内粒子离开斜边AD的最大距离
（3）第3秒内粒子能否离开斜劈？若能离开，离开时的速度多大？若不能离开，第3秒末的速度多大？

查看答案和解析>>

光滑绝缘水平面上固定一个光滑绝缘的斜劈，有一带电小球，质量m=1×10^-9kg，电荷量q=-6.28×10⁸C，小球紧靠在斜劈表面上，如图甲所示．空间充满相互垂直的匀强磁场和匀强电场，磁场方向竖直向下，磁感应强度大小为B=0.1T，电场沿水平方向且与斜劈底边垂直，电场强度大小按图乙所示规律变化，规定图示电场强度的方向为正方向．小球从t=0时刻由静止开始沿D→A方向滑动．已知sinθ=0.1045，cosθ=0.9945（算中取π=3.14，sinθ=0.1，cosθ=1）．求
（1）第1秒末粒子的速度大小
（2）第2秒内粒子离开斜边AD的最大距离
（3）第3秒内粒子能否离开斜劈？若能离开，离开时的速度多大？若不能离开，第3秒末的速度多大？

查看答案和解析>>

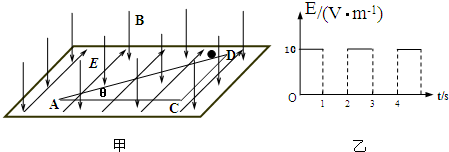
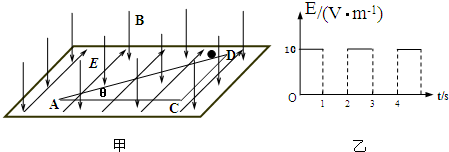
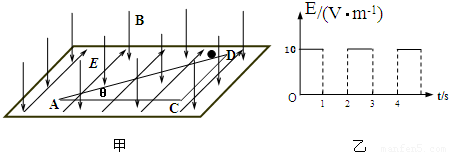
如图甲所示，由电磁感应现象形成的电源和平行板电容器相连接．电源内有固定的25匝线圈，穿过线圈的磁通量φ随时间t变化规律如乙图．平行板电容器两个极板水平放置，板间距离d＝2厘米．两极板间有一个带电微粒，质量m＝1.0×10^－6千克，带负电．电量为q＝1.8×10^－9库．假设t＝0时，上极板电势高，且此时带电微粒的瞬时速度为0，假设带电微粒的运动不会碰到极板．试求

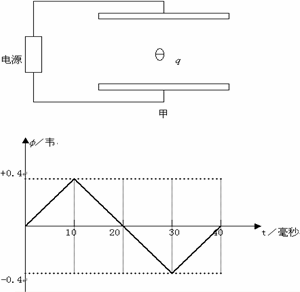
(1)微粒所受电场力是它重力的多少倍？

(2)微粒在30毫秒末的瞬时速度．

(3)微粒在30毫秒末相对于起始位置的位移．

查看答案和解析>>

1．D；解析：电子从低轨道向高轨道跃迁，需要吸收能量，这些能量和一部分动能转化为电子与原子核的势能

2．D；解析：的压缩量=（+）g/;的压缩量=g/；的伸长量'=g/；物块A上升的距离，物块B上升的距离

3．D；解析：当两列波的平衡位置在P点相遇时，P的位移就不是最大了。

4．A；解析：在M、N之间两者的场强方向都是向右的。由公式可知，因电量是4倍关系，则距离为2倍关系，两者场强大小才能相等。

5．D；解析：合上K的瞬间，L对两灯并没有影响，A、B同时亮。稳定后，L相当于导线，A更亮，B熄灭，①③错，②对；稳定后断开K，L相当于瞬时电源，A灯没有电流，B灯有L提供的瞬时电流，所以，A熄灭，B重新亮后再熄灭，④对。

6．A；解析：注意公式的条件（初速为零的匀变速的直线运动）。

7．D；解析：③错在半衰期随温度变化。

8．B；解析：光线入水到镜面，相当于白光进入三棱镜，折射后，光线分布是上红下紫。

9．B；解析：根据公式和已知条件，可以求出B正确。

10．B；解析：根据电磁感应的“阻碍”现象可以判断，两个线圈由于乙中电流变小而减小了吸引力，为了阻碍这个减小，甲中的电流应变大，又由于吸引力的作用，乙向左运动。

11．0.483；3.517；3.034

12．设计的电路：如答图1

答图1

13．不好（或不太好）

    根据电阻的定义：R＝知，U和I必须是电阻上的紧密关连的（或相互依存的）物理量，即：I必须是R两端电压降落为U值时，通过R的电流．

    如果先用伏特表测得待测电阻两端一个U值，后用电流表测得通过待测电阻的一个I值，对于一个确定的电源，由全电路欧姆定律知，测U时通过待测电阻的电流≠I，反之亦然．

14．（1）工作原理：电流在磁场中受安培力

    （2）＝I?h?B　①

    　 ②

15．（1）6×Wb；4×Wb

    （2）

    ∴　　

16．设轻绳长为l．B　开始运动时的加速度

    当B开始运动，位移为l时，速度大小为

    相互作用结束时的共同速度为，根据动量守恒　

    则

    绳绷直后的加速度

    B的总位移为s时的共同速度为，则．

    由以上关系式解出　l＝0.25m

17．两氘核进行对心碰撞，碰撞前后系统的动量守恒．碰撞前两氘核的动量之和为0，碰撞后设氦核和中子的动量分别是、，由动量守恒可得方程　

    题中说明核反应后所有结合能全部转化为机械能，则由能量守恒可得出核反应前后各粒子能量之间的关系式　由以上两方程再结合动量与动能之间的关系式便求得（1）问的解．

    （2）问中说明氦核沿直线向静止的核接近，就氦核和核组成的系统来说，因不受外力作用，故系统动量守恒．在库仑力作用下，两核距离最近时的物理意义是氦核和核的速度此时相等，因此可得一动量守恒方程．

    （1）反应中的质量亏损　＝2×2.0136-（3.0150＋1.0087）＝0.0035u

    所以释放的能量为　＝0.0035×931.5MeV＝3.26MeV

    设反应中生成的中子和氦核的速率分别为和由反应中能量守恒和动量守恒有

    其中＝0.35MeV

    由①得到

    所以动能之比为

    由②得到

    ∴　＝0.99MeV，＝2.97MeV

    （2）氦核与静止的碳核对心正碰后，当它们相距最近时，两核的速度相等，相当于完全非弹性碰撞模型，由动量守恒定律有　

    ∴　，此时，氦核的动能和碳核的动能分别为

    ≈0.04MeV

    ≈0.16MeV

18．在板壁面上，分子碰后等速反弹，在Dt时间内，共有：个分子产生碰撞（为阿佛伽德罗常数）

    由动量定理，产生的冲力为：FDt＝（2mv）DN

    即：F＝，其中m ＝44g/mo1为的摩尔质量．

    ∴　压强