
题目列表(包括答案和解析)
已知m>1,直线 ,椭圆C:
,椭圆C: ,
, 、
、 分别为椭圆C的左、右焦点.
分别为椭圆C的左、右焦点.
(Ⅰ)当直线过右焦点 时,求直线的方程;
时,求直线的方程;
(Ⅱ)设直线与椭圆C交于A、B两点,△A
 、△B
、△B
 的重心分别为G、H.若原点O在以线段GH为直径的圆内,求实数m的取值范围.[
的重心分别为G、H.若原点O在以线段GH为直径的圆内,求实数m的取值范围.[
【解析】第一问中因为直线 经过点
经过点 (
( ,0),所以
,0),所以 =
= ,得
,得 .又因为m>1,所以
.又因为m>1,所以 ,故直线的方程为
,故直线的方程为
第二问中设 ,由
,由 ,消去x,得
,消去x,得 ,
,
则由 ,知
,知 <8,且有
<8,且有
由题意知O为
 的中点.由
的中点.由 可知
可知 从而
从而 ,设M是GH的中点,则M(
,设M是GH的中点,则M( ).
).
由题意可知,2|MO|<|GH|,得到范围
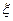 表示客人离开北京时游览的景点数与没有游览的景点数之差的绝对值.
表示客人离开北京时游览的景点数与没有游览的景点数之差的绝对值.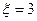 时的概率;
时的概率;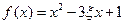 在区间
在区间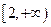 上是增函数”为事件A,求事件A的概率.
上是增函数”为事件A,求事件A的概率.已知等比数列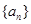 中,
中,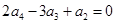 ,且
,且 ,公比
,公比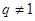 ,(1)求
,(1)求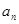 ;(2)设
;(2)设 ,求数列
,求数列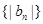 的前
的前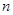 项和
项和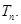
【解析】第一问,因为由题设可知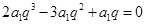
又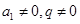 故
故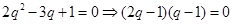
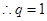 或
或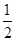 ,又由题设
,又由题设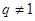
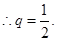 从而
从而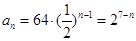
第二问中,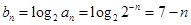
当 时,
时,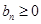 ,
, 时
时
故 时,
时,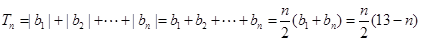
 时,
时,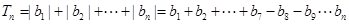
分别讨论得到结论。
由题设可知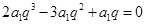
又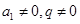 故
故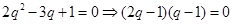
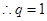 或
或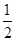 ,又由题设
,又由题设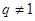
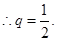
从而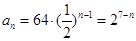 ……………………4分
……………………4分
(2)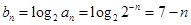
当 时,
时,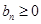 ,
, 时
时 ……………………6分
……………………6分
故 时,
时,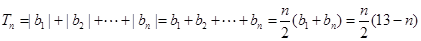 ……8分
……8分
 时,
时,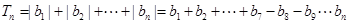
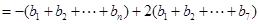
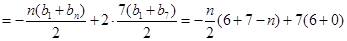
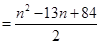 ……………………10分
……………………10分
综上可得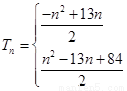

在等差数列{an}中,a1=3,其前n项和为Sn,等比数列{bn}的各项均为正数,b1=1,公比为q,且b2+ S2=12,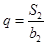 .(Ⅰ)求an 与bn;(Ⅱ)设数列{cn}满足
.(Ⅰ)求an 与bn;(Ⅱ)设数列{cn}满足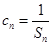 ,求{cn}的前n项和Tn.
,求{cn}的前n项和Tn.
【解析】本试题主要是考查了等比数列的通项公式和求和的运用。第一问中,利用等比数列{bn}的各项均为正数,b1=1,公比为q,且b2+ S2=12,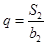 ,可得
,可得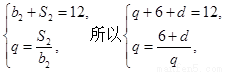 ,解得q=3或q=-4(舍),d=3.得到通项公式故an=3+3(n-1)=3n, bn=3 n-1. 第二问中,
,解得q=3或q=-4(舍),d=3.得到通项公式故an=3+3(n-1)=3n, bn=3 n-1. 第二问中,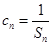 ,由第一问中知道
,由第一问中知道 ,然后利用裂项求和得到Tn.
,然后利用裂项求和得到Tn.
解: (Ⅰ) 设:{an}的公差为d,
因为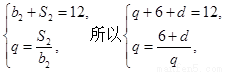 解得q=3或q=-4(舍),d=3.
解得q=3或q=-4(舍),d=3.
故an=3+3(n-1)=3n, bn=3 n-1. ………6分
(Ⅱ)因为 ……………8分
……………8分
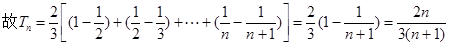
“肇实,正名芡实,因肇庆所产之芡实颗粒大、药力强,故名。”某科研所为进一步改良肇实,为此对肇实的两个品种(分别称为品种A和品种B)进行试验.选取两大片水塘,每大片水塘分成n小片水塘,在总共2n小片水塘中,随机选n小片水塘种植品种A,另外n小片水塘种植B.
(1)假设n=4,在第一大片水塘中,种植品种A的小片水塘的数目记为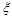 ,求
,求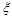 的分布列和数学期望;
的分布列和数学期望;
(2)试验时每大片水塘分成8小片,即n=8,试验结束后得到品种A和品种B在每个小片水塘上的每亩产量(单位:kg/亩)如下表:
|
号码 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
品种A |
101 |
97 |
92 |
103 |
91 |
100 |
110 |
106 |
|
品种B |
115 |
107 |
112 |
108 |
111 |
120 |
110 |
113 |
分别求品种A和品种B的每亩产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com