
题目列表(包括答案和解析)
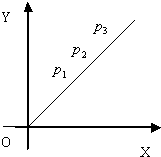 如图,在正比例函数y=kx(k>0)图象上有一列点P1,P2,P3,P4,…,Pn,….已知n≥2时,
如图,在正比例函数y=kx(k>0)图象上有一列点P1,P2,P3,P4,…,Pn,….已知n≥2时,| Pn-1Pn+1 |
Pn
|
| k | (x-1)2 |
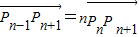 .设线段P1P2,P2P3,P3P4,…,PnPn+1的长分别为a1,a2,a3,…,an,且a1=1.
.设线段P1P2,P2P3,P3P4,…,PnPn+1的长分别为a1,a2,a3,…,an,且a1=1.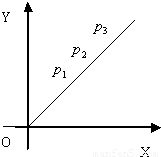
 )的图象上,如果存在,请求出点的坐标;如果不存在,请说明理由.
)的图象上,如果存在,请求出点的坐标;如果不存在,请说明理由.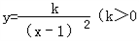 )的图象上,如果存在,请求出点的坐标;如果不存在,请说明理由。
)的图象上,如果存在,请求出点的坐标;如果不存在,请说明理由。湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com