
题目列表(包括答案和解析)
已知数列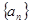 满足
满足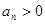 且对一切
且对一切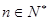 ,
,
有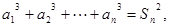
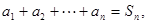
(Ⅰ)求证:对一切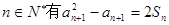
(Ⅱ)求数列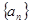 通项公式.
通项公式.
(Ⅲ)求证: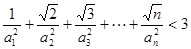
【解析】第一问利用,已知表达式,可以得到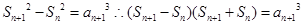 ,然后得到
,然后得到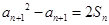 ,从而求证
。
,从而求证
。
第二问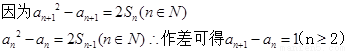 ,可得数列的通项公式。
,可得数列的通项公式。
第三问中,利用放缩法的思想,我们可以得到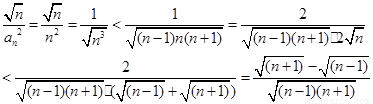
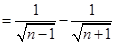 然后利用累加法思想求证得到证明。
然后利用累加法思想求证得到证明。
解: (1) 证明:
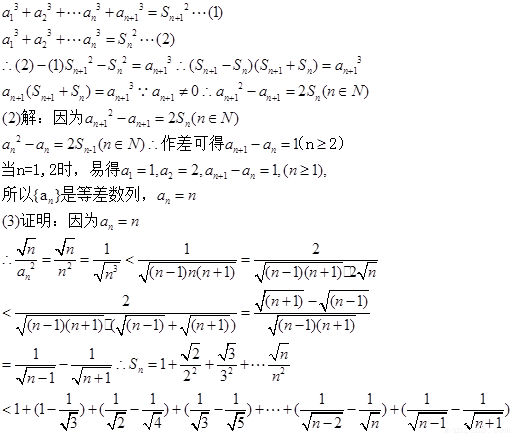
| 2 |
| 3 |
| 4 |
| 15 |
| 6 |
| 35 |
| 8 |
| 63 |
| 10 |
| 99 |
数列{an}的前n项和Sn=3n2+n+1,则此数列的通项公
式为 。
下列可作为数列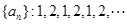 的通项公式的是 ( )
的通项公式的是 ( )
A.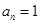 | B.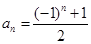 |
C.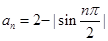 | D.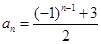 |
下列可作为数列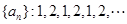 的通项公式的是 ( )
的通项公式的是 ( )
A.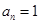 B.
B.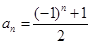
C.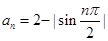 D.
D.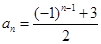
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com