
题目列表(包括答案和解析)
改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村 到
到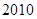 年十年间每年考入大学的人数.为方便计算,
年十年间每年考入大学的人数.为方便计算, 年编号为
年编号为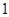 ,
,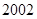 年编号为
年编号为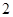 ,…,
,…,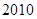 年编号为
年编号为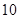 .数据如下:
.数据如下:
|
年份( |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
人数( |
3 |
5 |
8 |
11 |
13 |
14 |
17 |
22 |
30 |
31 |
(1)从这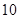 年中随机抽取两年,求考入大学的人数至少有
年中随机抽取两年,求考入大学的人数至少有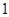 年多于
年多于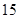 人的概率;
人的概率;
(2)根据前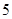 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出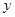 关于
关于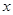 的回归方程
的回归方程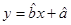 ,并计算第
,并计算第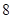 年的估计值和实际值之间的差的绝对值。
年的估计值和实际值之间的差的绝对值。
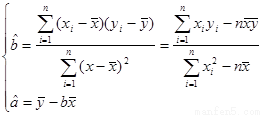
【解析】(1)设考入大学人数至少有1年多于15人的事件为A则P(A)=1-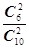 =
=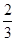 (4’)
(4’)
(2)由已知数据得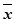 =3,
=3,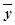 =8,
=8,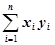 =3+10+24+44+65=146
=3+10+24+44+65=146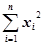 =1+4+9+16+25=55(7’)
=1+4+9+16+25=55(7’)
则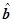 =
=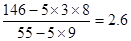 ,
,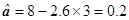 (9’)
(9’)
则回归直线方程为y=2.6x+0.2 (10’)
则第8年的估计值和真实值之间的差的绝对值为
已知实数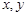 满足
满足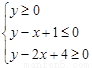 ,若
,若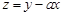 取得最大值时的最优解
取得最大值时的最优解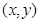 有无
有无
数个,则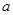 的值为( )
的值为( )
A.2 B.1 C.0 D.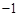
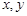 满足
满足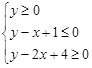 ,若
,若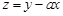 取得最大值时的最优解
取得最大值时的最优解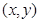 有无
有无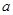 的值为( )
的值为( )| A.2 | B.1 | C.0 | D.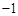 |
变量![]() 满足线性约束条件
满足线性约束条件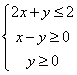 ,则使目标函数
,则使目标函数![]() 取得最大值的最优解有无数个,则
取得最大值的最优解有无数个,则![]() 的值为 .
的值为 .
已知实数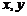 满足
满足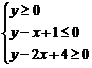 ,若
,若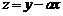
取得最大值时的最优解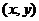 有无数个,则
有无数个,则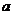 的值为
( )
的值为
( )
A.2 B.1 C.0 D.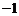
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com