
题目列表(包括答案和解析)
已知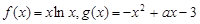
(1)求函数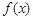 在
在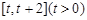 上的最小值
上的最小值
(2)对一切的 恒成立,求实数a的取值范围
恒成立,求实数a的取值范围
(3)证明对一切 ,都有
,都有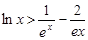 成立
成立
【解析】第一问中利用
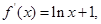 当
当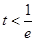 时,
时,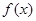 在
在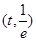 单调递减,在
单调递减,在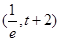 单调递增
单调递增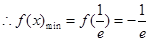 ,当
,当
 ,即
,即 时,
时,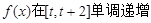 ,
,
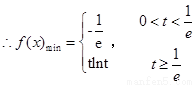
第二问中,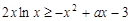 ,则
,则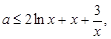 设
设 ,
,
则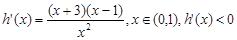 ,
, 单调递增,
单调递增, ,
, ,
, 单调递减,
单调递减,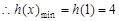 ,因为对一切
,因为对一切 ,
,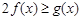 恒成立,
恒成立,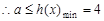
第三问中问题等价于证明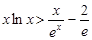 ,
, ,
,
由(1)可知 ,
, 的最小值为
的最小值为 ,当且仅当x=
,当且仅当x= 时取得
时取得
设 ,
, ,则
,则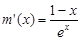 ,易得
,易得
 。当且仅当x=1时取得.从而对一切
。当且仅当x=1时取得.从而对一切 ,都有
,都有 成立
成立
解:(1)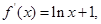 当
当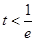 时,
时,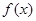 在
在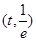 单调递减,在
单调递减,在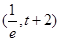 单调递增
单调递增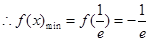 ,当
,当
 ,即
,即 时,
时,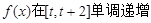 ,
,
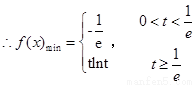 …………4分
…………4分
(2)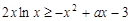 ,则
,则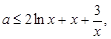 设
设 ,
,
则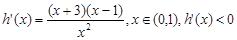 ,
, 单调递增,
单调递增, ,
, ,
, 单调递减,
单调递减,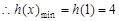 ,因为对一切
,因为对一切 ,
,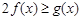 恒成立,
恒成立,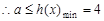 …………9分
…………9分
(3)问题等价于证明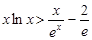 ,
, ,
,
由(1)可知 ,
, 的最小值为
的最小值为 ,当且仅当x=
,当且仅当x= 时取得
时取得
设 ,
, ,则
,则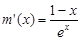 ,易得
,易得
 。当且仅当x=1时取得.从而对一切
。当且仅当x=1时取得.从而对一切 ,都有
,都有 成立
成立
已知 ,设
,设
 和
和 是方程
是方程 的两个根,不等式
的两个根,不等式 对任意实数
对任意实数 恒成立;
恒成立; 函数
函数 有两个不同的零点.求使“P且Q”为真命题的实数
有两个不同的零点.求使“P且Q”为真命题的实数 的取值范围.
的取值范围.
【解析】本试题主要考查了命题和函数零点的运用。由题设x1+x2=a,x1x2=-2,
∴|x1-x2|= =
= .
.
当a∈[1,2]时, 的最小值为3. 当a∈[1,2]时,
的最小值为3. 当a∈[1,2]时, 的最小值为3.
的最小值为3.
要使|m-5|≤|x1-x2|对任意实数a∈[1,2]恒成立,只须|m-5|≤3,即2≤m≤8.
由已知,得f(x)=3x2+2mx+m+ =0的判别式
=0的判别式
Δ=4m2-12(m+ )=4m2-12m-16>0,
)=4m2-12m-16>0,
得m<-1或m>4.
可得到要使“P∧Q”为真命题,只需P真Q真即可。
解:由题设x1+x2=a,x1x2=-2,
∴|x1-x2|= =
= .
.
当a∈[1,2]时, 的最小值为3.
的最小值为3.
要使|m-5|≤|x1-x2|对任意实数a∈[1,2]恒成立,只须|m-5|≤3,即2≤m≤8.
由已知,得f(x)=3x2+2mx+m+ =0的判别式
=0的判别式
Δ=4m2-12(m+ )=4m2-12m-16>0,
)=4m2-12m-16>0,
得m<-1或m>4.
综上,要使“P∧Q”为真命题,只需P真Q真,即
解得实数m的取值范围是(4,8]
已知函数 .
.
(1)试求 的值域;
的值域;
(2)设 ,若对
,若对 ,
,
 ,恒
,恒 成立,试求实数
成立,试求实数 的取值范围
的取值范围
【解析】第一问利用

第二问中若 ,则
,则 ,即当
,即当 时,
时, ,又由(Ⅰ)知
,又由(Ⅰ)知
若对 ,
, ,恒有
,恒有 成立,即
成立,即
 转化得到。
转化得到。
解:(1)函数可化为 ,
, ……5分
……5分
(2) 若 ,则
,则 ,即当
,即当 时,
时, ,又由(Ⅰ)知
,又由(Ⅰ)知 . …………8分
. …………8分
若对 ,
, ,恒有
,恒有 成立,即
成立,即
 ,
,

 ,即
,即 的取值范围是
的取值范围是
甲说:“只须不等式左边的最小值不小于右边的最大值”.
乙说:“把不等式变形为左边含变量![]() 的函数,右边仅含常数,求函数的最值”.
的函数,右边仅含常数,求函数的最值”.
丙说:“把不等式两边看成关于![]() 的函数,作出函数图像”.
的函数,作出函数图像”.
参考上述解题思路,你认为他们所讨论的问题的正确结论,即![]() 的取值范围是 .
的取值范围是 .
三个同学对问题“关于![]() 的不等式
的不等式![]() +25+|
+25+|![]() -5
-5![]() |≥
|≥![]() 在[1,12]上恒成立,求实数
在[1,12]上恒成立,求实数![]() 的取值范围”提出各自的解题思路.
的取值范围”提出各自的解题思路.
甲说:“只须不等式左边的最小值不小于右边的最大值”.
乙说:“把不等式变形为左边含变量![]() 的函数,右边仅含常数,求函数的最值”.
的函数,右边仅含常数,求函数的最值”.
丙说:“把不等式两边看成关于![]() 的函数,作出函数图像”.
的函数,作出函数图像”.
参考上述解题思路,你认为他们所讨论的问题的正确结论,即![]() 的取值范围是 .
的取值范围是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com