
题目列表(包括答案和解析)
函数 的定义域关于原点对称,但不包括数0,对定义域中的任意实数
的定义域关于原点对称,但不包括数0,对定义域中的任意实数 ,在定义域中存在
,在定义域中存在 使
使 ,
, ,且满足以下3个条件。
,且满足以下3个条件。
(1) 是
是 定义域中的数,
定义域中的数, ,则
,则
(2) ,(
,( 是一个正的常数)
是一个正的常数)
(3)当 时,
时, 。
。
证明:(1) 是奇函数;
是奇函数;
(2) 是周期函数,并求出其周期;
是周期函数,并求出其周期;
(3) 在
在 内为减函数。
内为减函数。
函数 的定义域关于原点对称,但不包括数0,对定义域中的任意实数
的定义域关于原点对称,但不包括数0,对定义域中的任意实数 ,在定义域中存在
,在定义域中存在 使
使 ,
, ,且满足以下3个条件。
,且满足以下3个条件。
(1) 是
是 定义域中的数,
定义域中的数, ,则
,则
(2) ,(
,( 是一个正的常数)
是一个正的常数)
(3)当 时,
时, 。
。
证明:(1) 是奇函数;
是奇函数;
(2) 是周期函数,并求出其周期;
是周期函数,并求出其周期;
(3) 在
在 内为减函数。
内为减函数。
已知函数
(1)若函数 的图象经过P(3,4)点,求a的值;
的图象经过P(3,4)点,求a的值;
(2)比较 大小,并写出比较过程;
大小,并写出比较过程;
(3)若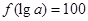 ,求a的值.
,求a的值.
【解析】本试题主要考查了指数函数的性质的运用。第一问中,因为函数 的图象经过P(3,4)点,所以
的图象经过P(3,4)点,所以 ,解得
,解得 ,因为
,因为 ,所以
,所以 .
.
(2)问中,对底数a进行分类讨论,利用单调性求解得到。
(3)中,由 知,
知, .,指对数互化得到
.,指对数互化得到 ,,所以
,,所以 ,解得所以,
,解得所以, 或
或  .
.
解:⑴∵函数 的图象经过
的图象经过 ∴
∴ ,即
,即 . … 2分
. … 2分
又 ,所以
,所以 .
………… 4分
.
………… 4分
⑵当 时,
时, ;
;
当 时,
时, . ……………… 6分
. ……………… 6分
因为, ,
,
当 时,
时, 在
在 上为增函数,∵
上为增函数,∵ ,∴
,∴ .
.
即 .当
.当 时,
时, 在
在 上为减函数,
上为减函数,
∵ ,∴
,∴ .即
.即 . …………………… 8分
. …………………… 8分
⑶由 知,
知, .所以,
.所以, (或
(或 ).
).
∴ .∴
.∴ , … 10分
, … 10分
∴ 或
或
 ,所以,
,所以, 或
或  .
.
已知![]() ,且
,且![]()
1.设![]() ,求
,求![]() 的解析式;
的解析式;
2.设![]() ,试问:是否存在实数
,试问:是否存在实数![]() ,使
,使![]() 在
在![]() 内为减函数,且在(-1,0)内是增函数.
内为减函数,且在(-1,0)内是增函数.
当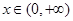 时,幂函数
时,幂函数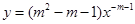 为减函数,则实数
为减函数,则实数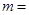 ( )
( )
A.m=2
B.m=-1 C.m=2或m=-1 D.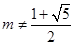
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com