练习册

  • 练习册
  • 试题
    18．已知空间二点A, 设, . 【查看更多】

     

    题目列表(包括答案和解析)

    已知直三棱柱中, , ， 是和的交点, 若.

    （1）求的长；  （2）求点到平面的距离；

    （3）求二面角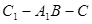的平面角的正弦值的大小.

    【解析】本试题主要考查了距离和角的求解运用。第一问中，利用ACCA为正方形, AC=3

    第二问中，利用面BBCC内作CDBC, 则CD就是点C平面ABC的距离CD=，第三问中，利用三垂线定理作二面角的平面角，然后利用直角三角形求解得到其正弦值为

    解法一: (1)连AC交AC于E, 易证ACCA为正方形, AC=3 ……………  5分

    (2)在面BBCC内作CDBC, 则CD就是点C平面ABC的距离CD= … 8分

    (3) 易得AC面ACB, 过E作EHAB于H, 连HC, 则HCAB

    CHE为二面角C－AB－C的平面角. ………  9分

    sinCHE=二面角C－AB－C的平面角的正弦大小为 ……… 12分

    解法二: (1)分别以直线CB、CC、CA为x、y为轴建立空间直角坐标系, 设|CA|=h, 则C(0, 0, 0), B(4, 0, 0), B(4, －3, 0), C(0, －3, 0), A(0, 0, h), A(0, －3, h), G(2, －, －) ………………………  3分

    =(2, －, －), =(0, －3, －h)  ……… 4分

    ·=0,  h=3

    (2)设平面ABC得法向量=(a, b, c),则可求得=(3, 4, 0) (令a=3)

    点A到平面ABC的距离为H=||=……… 8分

    (3) 设平面ABC的法向量为=(x, y, z),则可求得=(0, 1, 1) (令z=1)

    二面角C－AB－C的大小满足cos== ………  11分

    二面角C－AB－C的平面角的正弦大小为

     

    查看答案和解析>>

    一、选择题（本大题共10小题，每小题5分，共50分，每题只有一个正确选项）

    题号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    答案

     

    C

    A

    B

    A

    D

    B

    D

    A

    C

    D

    二、填空题（本大题共有5小题，每小题4分，共20分）

    11. (1,0)      12. 1/2      13.6ec8aac122bd4f6e/9      14. (-1/4,1)    15. 6ec8aac122bd4f6e     

    三、解答题（本大题共有5小题，满分50分，解答应写出文字说明证明过程或演算步骤）

    16．(本小题满分8分)

    解：  因为6ec8aac122bd4f6e，所以－2<m<2；……………………………………1分

    若方程6ec8aac122bd4f6e无实根，则6ec8aac122bd4f6e，  ……2分

    即6ec8aac122bd4f6e，    所以q:1<m<3． ……………………………………3分

        因为┲p为假，则p为真，又因为p∧q为假，则q为假．   ……………………5分

    所以6ec8aac122bd4f6e……………………7分

        所以-2<m≤1．故实数6ec8aac122bd4f6e的取值范围为6ec8aac122bd4f6e．    ………………………………8分

    17．（本小题满分10分）

    解：（1）将6ec8aac122bd4f6e代入6ec8aac122bd4f6e，消去6ec8aac122bd4f6e，

    整理得6ec8aac122bd4f6e．        ………………………………2分

    因为直线6ec8aac122bd4f6e与椭圆6ec8aac122bd4f6e相交于6ec8aac122bd4f6e两个不同的点，

    所以6ec8aac122bd4f6e，……………………4分

     解得6ec8aac122bd4f6e．所以6ec8aac122bd4f6e的取值范围为6ec8aac122bd4f6e．………………………6分

    (2) 解法1：设6ec8aac122bd4f6e,由⑴知6ec8aac122bd4f6e……7分

    ∵弦6ec8aac122bd4f6e的中点6ec8aac122bd4f6e的横坐标是-6ec8aac122bd4f6e，∴6ec8aac122bd4f6e…………………8分

    ∴b=1∈6ec8aac122bd4f6e……10分

    解法2：设6ec8aac122bd4f6e,6ec8aac122bd4f6e    由6ec8aac122bd4f6e，6ec8aac122bd4f6e

    作差得6ec8aac122bd4f6e    (*)

    因为6ec8aac122bd4f6e，6ec8aac122bd4f6e   …………………8分

    代入(*)得 6ec8aac122bd4f6e ∴中点6ec8aac122bd4f6e的纵坐标是6ec8aac122bd4f6e，

    代入6ec8aac122bd4f6e得b=1∈6ec8aac122bd4f6e……10分

    18．（本小题满分10分）

    解(1) ∵6ec8aac122bd4f6e=6ec8aac122bd4f6e-6ec8aac122bd4f6e=6ec8aac122bd4f6e-6ec8aac122bd4f6e=(-2,-1,2),

    ∵6ec8aac122bd4f6e∥6ec8aac122bd4f6e   ∴ 设6ec8aac122bd4f6e………2分

    ∴6ec8aac122bd4f6e＝6ec8aac122bd4f6e  ∴t=±1,   …………………4分

    ∴6ec8aac122bd4f6e或6ec8aac122bd4f6e………………………………5分

    (2) k6ec8aac122bd4f6e+6ec8aac122bd4f6e＝（k-1，k，2），k6ec8aac122bd4f6e-26ec8aac122bd4f6e＝（k+2，k，-4）………………………………6分

    又（k6ec8aac122bd4f6e+6ec8aac122bd4f6e）⊥（k6ec8aac122bd4f6e-26ec8aac122bd4f6e）     所以 （k6ec8aac122bd4f6e+6ec8aac122bd4f6e）?（k6ec8aac122bd4f6e-26ec8aac122bd4f6e）＝0…………………7分

    ∴（k-1，k，2）?（k+2，k，-4）＝6ec8aac122bd4f6e…………………………9分

    ∴6ec8aac122bd4f6e或6ec8aac122bd4f6e                          ………………………………10分

    19．（本小题满分10分）

    方法一：证：（Ⅰ）在Rt△BAD中，AD=2，BD=6ec8aac122bd4f6e， ∴AB=2，

    ABCD为正方形，因此BD⊥AC. ∵PA⊥平面ABCD，BDÌ平面ABCD，∴BD⊥PA  

    又∵PA∩AC=A   ∴BD⊥平面PAC.            ………………………………3分

    解：（Ⅱ）作AH⊥PB于H，连结DH，∵PA⊥AD，AB⊥AD，∴DA⊥平面PAB，∴DH⊥PB，∴∠AHD为二面角A－PB－D的平面角.    ……………………………5分

     又∵PA=AB，∴H是PB中点，∴AH＝6ec8aac122bd4f6e，DH＝6ec8aac122bd4f6e∴cos∠AHD=AH/DH=6ec8aac122bd4f6e/ 6ec8aac122bd4f6e=6ec8aac122bd4f6e.∴二面角A－PB－D的余弦值是6ec8aac122bd4f6e ………………………………7分

    （Ⅲ）∵PA=AB=AD=2，∴PB=PD=BD=6ec8aac122bd4f6e ，设C到面PBD的距离为d，

    6ec8aac122bd4f6e由6ec8aac122bd4f6e，有6ec8aac122bd4f6e，                        

    即6ec8aac122bd4f6e，

    得6ec8aac122bd4f6e     ………………………………10分  

    方法二：证：（Ⅰ）建立如图所示的直角坐标系，

    则A（0，0，0）、D（0，2，0）、P（0，0，2）.

    在Rt△BAD中，AD=2，BD=6ec8aac122bd4f6e，

    ∴AB=2.∴B（2，0，0）、C（2，2，0），

    ∴6ec8aac122bd4f6e   ……………………………1分

    ∵6ec8aac122bd4f6e，即BD⊥AP，BD⊥AC，又AP∩AC=A，

    ∴BD⊥平面PAC.                               ………………………………3分

    解：（Ⅱ）由（Ⅰ）得6ec8aac122bd4f6e.

    设平面PBD的法向量为6ec8aac122bd4f6e，则6ec8aac122bd4f6e，

    即6ec8aac122bd4f6e，∴6ec8aac122bd4f6e  故平面PBD的法向量可取为6ec8aac122bd4f6e  ……5分

    ∵DA⊥平面ABCD，∴6ec8aac122bd4f6e为平面PAD的法向量.       ………………6分

    设二面角A－PB－D的大小为q，依题意可得6ec8aac122bd4f6e，∴二面角A－PB－D的余弦值是6ec8aac122bd4f6e.…………7分

    （Ⅲ）∵6ec8aac122bd4f6e，又由（Ⅱ）得平面PBD的法向量为6ec8aac122bd4f6e.…………8分

    ∴C到面PBD的距离为6ec8aac122bd4f6e   ………………10分

     

     

    20、（本小题满分12分）

    （1）设N（x，y），由题意“过点6ec8aac122bd4f6e作6ec8aac122bd4f6e交6ec8aac122bd4f6e轴于点6ec8aac122bd4f6e，点M关于点P的对称点是6ec8aac122bd4f6e”得6ec8aac122bd4f6e   ………………2分

    ∴6ec8aac122bd4f6e＝（-x,-6ec8aac122bd4f6e）, 6ec8aac122bd4f6e＝（1,-6ec8aac122bd4f6e）               ……………………………4分

    由6ec8aac122bd4f6e?6ec8aac122bd4f6e=0得6ec8aac122bd4f6e                           ……………………………5分

    （2）设L与抛物线交于点6ec8aac122bd4f6e，

    则由6ec8aac122bd4f6e，得6ec8aac122bd4f6e，             ……………………………6分

    由点A、B在抛物线6ec8aac122bd4f6e上有6ec8aac122bd4f6e，故6ec8aac122bd4f6e………7分

    当L与X轴垂直时，则由6ec8aac122bd4f6e，得6ec8aac122bd4f6e，

    不合题意，故L与X轴不垂直。                     ………………………… ……8分

    可设直线L的方程为y=kx+b(k≠0)

    又由6ec8aac122bd4f6e，6ec8aac122bd4f6e，得6ec8aac122bd4f6e

    所以6ec8aac122bd4f6e                           ………………………………10分

    6ec8aac122bd4f6e，因为6ec8aac122bd4f6e

    所以   96＜6ec8aac122bd4f6e＜480             ………………………………11分

    解得直线L的斜率取值范围为（-1，-6ec8aac122bd4f6e）∪ （6ec8aac122bd4f6e，1）………………………………12分

     

    （其他方法酌情给分）

     

     

    命题学校：瑞安四中（65531798） 命题人：薛孝西（13967706784）

    审核学校：洞头一中（63476763） 审核人：陈  健（13968901086）

     


    同步练习册答案