
题目列表(包括答案和解析)
16.(2)解(1)当a=1,b=-2时,g(x)=f(x)-2,把f(x)图象向下平移两个单位就可得到g(x)图象,
这时函数g(x)只有两个零点,所以(1)不对
(2)若a=-1,-2<b<0,则把函数f(x)作关于x轴对称图象,然后向下平移不超过2个单位就可得到g(x)图象,这时g(x)有超过2的零点
(3)当a<0时, y=af(x)根据定义可断定是奇函数,如果b≠0,把奇函数y=af(x)图象再向上(或向下)平移后才是y=g(x)=af(x)+b的图象,那么肯定不会再关于原点对称了,肯定不是奇函数;当b=0时才是奇函数,所以(3)不对。所以正确的只有(2)
为了考察高中生学习语文与数学之间的关系,在某中学学生中随机地抽取了610名学生得到如下列表:
|
数学 | 及格 | 不及格 | 总计 |
| 及格 | 310 | 142 | 452 |
| 不及格 | 94 | 64 | 158 |
| 总计 | 404 | 206 | 610 |
由表中数据计算及![]() 的观测值
的观测值![]() 问在多大程度上可以认为高中生的语文与数学成绩之间有关系?为什么?
问在多大程度上可以认为高中生的语文与数学成绩之间有关系?为什么?
 已知y=x(x-1)(x+1)的图像如图所示,今考虑f(x)=x(x-1)(x+1)+0.01,对于方程式f(x)=0根的情况,以下说法正确的是________.(填上正确的序号)
已知y=x(x-1)(x+1)的图像如图所示,今考虑f(x)=x(x-1)(x+1)+0.01,对于方程式f(x)=0根的情况,以下说法正确的是________.(填上正确的序号)
①有三个实根;
②当x<-1时,恰有一实根;
③当-1<x<0时,恰有一实根;
④当0<x<1时,恰有一实根;
⑤当x>1时,恰有一实根.
(09年东城区示范校质检一文)(14分)
设函数![]() 的定义域为全体R,当x<0时,
的定义域为全体R,当x<0时,![]() ,且对任意的实数x,y∈R,有
,且对任意的实数x,y∈R,有![]() 成立,数列
成立,数列![]() 满足
满足![]() ,且
,且![]() (n∈N*)
(n∈N*)
(Ⅰ)求证:![]() 是R上的减函数;
是R上的减函数;
(Ⅱ)求数列![]() 的通项公式;
的通项公式;
(Ⅲ)若不等式![]() 对一切n∈N*均成立,求k的
对一切n∈N*均成立,求k的
最大值.
已知y=x(x-1)(x+1)的图像如图所示,今考虑f(x)=x(x-1)(x+1)+0.01,对于方程式f(x)=0根的情况,以下说法正确的是________.(填上正确的序号)
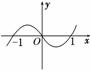 ①有三个实根;
①有三个实根;
②当x<-1时,恰有一实根;
③当-1<x<0时,恰有一实根;
④当0<x<1时,恰有一实根;
⑤当x>1时,恰有一实根.
(本小题满分12分) 设函数f(x)的定义域是R,对于任意实数m,n,恒有f(m+n)=f(m)f(n),且当x>0时,0<f(x)<1。
(1)求证:f(0)=1,且当x<0时,有f(x)>1;
(2)判断f(x)在R上的单调性;
⑶设集合A={(x,y)|f(x2)f(y2)>f(1)},集合B={(x,y)|f(ax-y+2)=1,a∈R},若A∩B=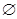 ,求a的取值范围。
,求a的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com