
题目列表(包括答案和解析)
(本小题满分14分)设椭圆 与抛物线
与抛物线 的焦点均在
的焦点均在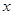 轴上,
轴上, 的中心和
的中心和 的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中:
的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1)求 ,
, 的标准方程, 并分别求出它们的离心率
的标准方程, 并分别求出它们的离心率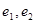 ;
;
2)设直线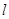 与椭圆
与椭圆 交于不同的两点
交于不同的两点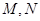 ,且
,且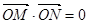 (其中
(其中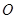 坐标原点),请问是否存在这样的直线
坐标原点),请问是否存在这样的直线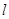 过抛物线
过抛物线 的焦点
的焦点 若存在,求出直线
若存在,求出直线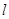 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(本小题满分14分)设椭圆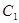 与抛物线
与抛物线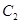 的焦点均在
的焦点均在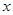 轴上,
轴上,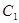 的中心和
的中心和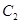 的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中:
的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中:
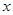 |  |  |  |  |  |
 |  |  |  |  |  |
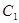 ,
,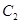 的标准方程, 并分别求出它们的离心率
的标准方程, 并分别求出它们的离心率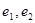 ;
; 与椭圆
与椭圆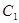 交于不同的两点
交于不同的两点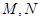 ,且
,且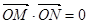 (其中
(其中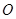 坐标原点),请问是否存在这样的直线
坐标原点),请问是否存在这样的直线 过抛物线
过抛物线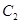 的焦点
的焦点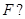 若存在,求出直线
若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.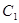 与抛物线
与抛物线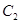 的焦点均在
的焦点均在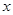 轴上,
轴上,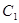 的中心和
的中心和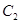 的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中:
的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中: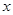 |  |  |  |  | 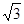 |
 |  |  |  |  |  |
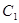 ,
,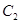 的标准方程, 并分别求出它们的离心率
的标准方程, 并分别求出它们的离心率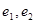 ;
;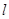 与椭圆
与椭圆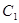 交于不同的两点
交于不同的两点 ,且
,且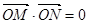 (其中
(其中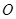 坐标原点),请问是否存在这样的直线
坐标原点),请问是否存在这样的直线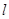 过抛物线
过抛物线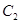 的焦点
的焦点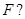 若存在,求出直线
若存在,求出直线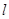 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.(本小题满分14分)已知![]() 抛物线
抛物线![]()
(1)设![]() 是C1的任意两条互相垂直的切线,并设
是C1的任意两条互相垂直的切线,并设![]() ,证明
,证明![]() :点M的纵坐标为定值;
:点M的纵坐标为定值;![]()
(2)在C1上是否存在点P,使得C1在点P处切线与C2相交于两点A、B,且AB的中垂线恰为C1的切线?若存在,求出点P的坐标;若不存在,说明理由。
(本小题满分14分)某城市自西向东和自南向北的两条主干道的东南方位有一块空地市规划部门计划利用它建设一个供市民休闲健身的小型绿化广场,如下图所示是步行小道设计方案示意图,

其中, 分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点
分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点 处修一条步行小道,小道为抛物线
处修一条步行小道,小道为抛物线 的一段,在小道上依次以点
的一段,在小道上依次以点
 为圆心,修一系列圆型小道,这些圆型小道与主干道
为圆心,修一系列圆型小道,这些圆型小道与主干道 相切,且任意相邻的两圆彼此外切,若
相切,且任意相邻的两圆彼此外切,若 (单位:百米)且
(单位:百米)且 .
.
(1)记以 为圆心的圆与主干道
为圆心的圆与主干道 切于
切于 点,证明:数列
点,证明:数列 是等差数列,并求
是等差数列,并求 关于
关于 的表达式;
的表达式;
(2)记 的面积为
的面积为 ,根据以往施工经验可知,面积为
,根据以往施工经验可知,面积为 的圆型小道的施工工时为
的圆型小道的施工工时为 (单位:周).试问5周时间内能否完成前
(单位:周).试问5周时间内能否完成前 个圆型小道的修建?请说明你的理由.
个圆型小道的修建?请说明你的理由.
一、DBBCA,CCBCD,BA
二、13、3,14、,15、x+y-2=0,16、12
三、解答题:
17.解:∵……………2分 ………4分
…………………………………………6分
……………………………8分
………………………………………………10分
又 ∴………………………12分
18.解:(Ⅰ)记甲、乙、丙三台机器在一小时需要照顾分别为事件A、B、C,……1分
则A、B、C相互独立,
由题意得: P(AB)=P(A)?P(B)=0.05
P(AC)=P(A)?P(C)=0.1
P(BC)=P(B)?P(C)=0.125…………………………………………………………4分
解得:P(A)=0.2;P(B)=0.25;P(C)=0.5
所以, 甲、乙、丙每台机器在这个小时内需要照顾的概率分别是0.2、0.25、0.5……6分
(Ⅱ)∵A、B、C相互独立,∴相互独立,……………………………………7分
∴甲、乙、丙每台机器在这个小时内需都不需要照顾的概率为
…………………………10分
∴这个小时内至少有一台需要照顾的概率为
……12分
19.证明:(Ⅰ)作AD的中点O,则VO⊥底面
ABCD.…………………………1分
建立如图空间直角坐标系,并设正方形边长为1,…………………………2分
则A(,0,0),B(,1,0),C(-,1,0),D(-,0,0),V(0,0,),
∴………………………………3分
由……………………………………4分
……………………………………5分
又AB∩AV=A ∴AB⊥平面VAD…………………………………………6分
(Ⅱ)由(Ⅰ)得是面VAD的法向量………………………………7分
设是面VDB的法向量,则
……9分
∴,……………………………………11分
又由题意知,面VAD与面VDB所成的二面角,所以其大小为…………12分
20.解:由题意得:……………1分 即…………3分
又…………4分 又成等比数列,
∴该数列的公比为,………6分 所以………8分
又……………………………………10分
所以数列的通项为……………………………12分
21.解:设容器的高为x,容器的体积为V,……………………………………………1分
则V=(90-2x)(48-2x)x,(0<V<24)………………………………………………5分
=4x3-276x2+4320x ∵V′=12 x2-552x+4320………………………………7分
由V′=12 x2-552x+4320=0得x1=10,x2=36
∵x<10 时,V′>0, 10<x<36时,V′<0, x>36时,V′>0,
所以,当x=10,V有极大值V(10)=1960………………………………………10分
又V(0)=0,V(24)=0,………………………………………………………………11分
所以当x=10,V有最大值V(10)=1960……………………………………………12分
22.解:(Ⅰ)∵抛物线,即,
∴焦点为………………………………………………………1分
(1)直线的斜率不存在时,显然有………………………………3分
(2)直线的斜率存在时,设为k, 截距为b
即直线:y=kx+b 由已知得:
……………5分
……………7分
即的斜率存在时,不可能经过焦点……………………………………8分
所以当且仅当=0时,直线经过抛物线的焦点F…………………………9分
(Ⅱ)当时,
直线的斜率显然存在,设为:y=kx+b………………………………10分
则由(Ⅰ)得:
………………………11分
…………………………………………13分
所以直线的方程为,即………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com