
题目列表(包括答案和解析)
三、解答题:解答应写出文字说明、证明过程或演算步骤(本大题共6个大题,共76分)。
17.(12分)以下资料是一位销售经理收集来的每年销售额和销售经验年数的关系:
|
销售经验(年) |
1 |
3 |
4 |
4 |
6 |
8 |
10 |
10 |
11 |
13 |
|
年销售额(千元) |
80 |
97 |
92 |
102 |
103 |
111 |
119 |
123 |
117 |
136 |
(1)依据这些数据画出散点图并作直线 =78+4.2x,计算
=78+4.2x,计算 (yi-
(yi- i)2;
i)2;
(2)依据这些数据由最小二乘法求线性回归方程,并据此计算 ;
;
(3)比较(1)和(2)中的残差平方和 的大小.
的大小.
三、解答题:解答应写出文字说明、证明过程或演算步骤(本大题共6个大题,共76分)。
17.(12分)以下资料是一位销售经理收集来的每年销售额和销售经验年数的关系:
| 销售经验(年) | 1 | 3 | 4 | 4 | 6 | 8 | 10 | 10 | 11 | 13 |
| 年销售额(千元) | 80 | 97 | 92 | 102 | 103 | 111 | 119 | 123 | 117 | 136 |
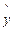 =78+4.2x,计算
=78+4.2x,计算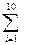 (yi-
(yi-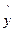 i)2;
i)2; 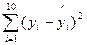 ;
;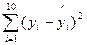 的大小.
的大小.甲乙两个学校高三年级分别有1100人,1000人,为了了解两个学校全体高三年级学生在该地区二模考试的数学成绩情况,采用分层抽样方法从两个学校一共抽取了105名学生的数学成绩,并作出了频数分布统计表如下:
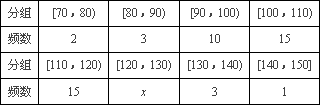
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 2 | 3 | 10 | 15 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 15 | x | 3 | 1 |
甲校:
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 1 | 2 | 9 | 8 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 10 | 10 | y | 3 |
乙校:
(Ⅰ)计算x,y的值。
| 甲校 | 乙校 | 总计 |
优秀 | |||
非优秀 | |||
总计 |
(Ⅱ)若规定考试成绩在[120,150]内为优秀,请分别估计两个学校数学成绩的优秀率;
(Ⅲ)由以上统计数据填写右面2×2列联表,并判断是否有97.5%的把握认为两个学校的数学成绩有差异。
P(k2>k0) | 0.10 | 0.025 | 0.010 |
K | 2.706 | 5.024 | 6.635 |
附:K2= ;
甲乙两个学校高三年级分别有1100人,1000人,为了了解两个学校全体高三年级学生在该地区二模考试的数学成绩情况,采用分层抽样方法从两个学校一共抽取了105名学生的数学成绩,并作出了频数分布统计表如下:
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 2 | 3 | 10 | 15 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 15 | x | 3 | 1 |
甲校:
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 1 | 2 | 9 | 8 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 10 | 10 | y | 3 |
乙校:
(Ⅰ)计算x,y的值。
(Ⅱ)若规定考试成绩在[120,150]内为优秀,请分别估计两个学校数学成绩的优秀率;
(Ⅲ)由以上统计数据填写右面2×2列联表,并判断是否有97.5%的把握认为两个学校的数学成绩有差异。
附:K2=![]() ;
;
|
| 甲校 | 乙校 | 总计 |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| P(k2>k0) | 0.10 | 0.025 | 0.010 |
| K | 2.706 | 5.024 | 6.635 |
甲乙两个学校高三年级分别有1100人,1000人,为了了解两个学校全体高三年级学生在该地区二模考试的数学成绩情况,采用分层抽样方法从两个学校一共抽取了105名学生的数学成绩,并作出了频数分布统计表如下:
甲校:
乙校:
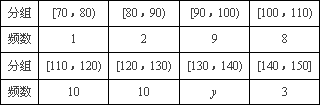
(Ⅰ)计算x,y的值.
(Ⅱ)若规定考试成绩在[120,150]内为优秀,请分别估计两个学校数学成绩的优秀率;
(Ⅲ)由以上统计数据填写下面2×2列联表,并判断是否有97.5%的把握认为两个学校的数学成绩有差异.
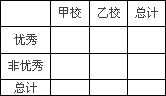
附:K2=![]() ;
;

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com