练习册

  • 练习册
  • 试题
    设实数a0.a.b满足 和 【查看更多】

     

    题目列表(包括答案和解析)

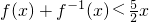    设函数f（x）的定义域、值域均为R，f（x）的反函数为f-1（x），且对任意实数x，均有数学公式，定义数列an：a0=8，a1=10，an=f（an-1），n=1，2，…．
    （1）求证：数学公式；
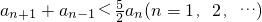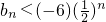    （2）设bn=an+1-2an，n=0，1，2，…．求证：数学公式（n∈N*）；
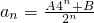    （3）是否存在常数A和B，同时满足①当n=0及n=1时，有数学公式成立；②当n=2，3，…时，有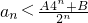数学公式成立．如果存在满足上述条件的实数A、B，求出A、B的值；如果不存在，证明你的结论．

    查看答案和解析>>

    已知函数满足下列条件：对任意的实数x1，x2都有  和，其中是大于0的常数.设实数a0，a，b满足 和.

           （Ⅰ）证明:，并且不存在，使得；

           （Ⅱ）证明:；

           （Ⅲ）证明:.

    查看答案和解析>>

    已知函数满足下列条件：对任意的实数x1，x2都有和，其中是大于0的常数.

    设实数a0，a，b满足  和

    (Ⅰ)证明，并且不存在，使得；

    (Ⅱ)证明；

    (Ⅲ)证明.

     

    查看答案和解析>>

    已知函数满足下列条件：对任意的实数x1，x2都有λ(x1－x2)2≤(x1－x2)[f(x1)－f(x2)]和|f(x1)－f(x2)|≤|x1－x2|，其中λ是大于0的常数．设实数a0，a，b满足f(a0)=0和b=a－λf(a)

    (Ⅰ)证明λ≤1，并且不存在b0≠a0，使得f(b0)=0；

    (Ⅱ)证明(b－a0)2≤(1－λ2)(a－a0)2；

    (Ⅲ)证明[f(b)]2≤(1－λ2)[f(a)]2．

    查看答案和解析>>

    已知函数满足下列条件：对任意的实数x1，x2都有和，其中是大于0的常数.

    设实数a0，a，b满足  和

    (Ⅰ)证明，并且不存在，使得；

    (Ⅱ)证明；

    (Ⅲ)证明.

     

    查看答案和解析>>

     

    一、选择题：本题考查基本知识和基本运算，每小题5分，满分60分.

    （1）A      （2）B     （3）D     （4）C      （5）A    （6）B

    （7）C      （8）A     （9）D     （10）C     （11）B    （12）A

    二、填空题：本题考查基本知识和基本运算，每小题4分，满分16分.

    （13）                         （14）

    （15）2                                        （16）

    三、解答题

    （17）本小题主要考查三角函数的基本公式和三角函数的恒等变换等基本知识，以及推理能力和运算能力.满分12分.

          解：由已知.

      

          从而 

    .

    （18）本小题主要考查线面关系和正方体性质等基本知识，考查空间想象能力和推理论证能力.满分12分.

          解法一：（I）连结BP.

          ∵AB⊥平面BCC1B1，  ∴AP与平面BCC1B1所成的角就是∠APB,

          ∵CC1=4CP,CC1=4，∴CP=I.

          在Rt△PBC中，∠PCB为直角，BC=4，CP=1，故BP=.

          在Rt△APB中，∠ABP为直角，tan∠APB=

          ∴∠APB=

    （19）本小题主要考查简单线性规划的基本知识，以及运用数学知识解决实际问题的能力.满分12分.

          解：设投资人分别用x万元、y万元投资甲、乙两个项目.

          由题意知

          目标函数z=x+0.5y.

          上述不等式组表示的平面区域如图所示，阴影部分（含边界）即可行域.

          与可行域相交，其中有一条直线经过可行域上的M点，且

          与直线的距离最大，这里M点是直线

          和的交点.

           解方程组 得x=4，y=6

          此时（万元）.

              当x=4，y=6时z取得最大值.

          答：投资人用4万元投资甲项目、6万元投资乙项目，才能在确保亏损不超过1.8万元的前提下，使可能的盈利最大.

    （20）本小题主要考查数列的基本知识，以及运用数学知识分析和解决问题的能力.满分12分.

          解：（I）当时，

                 

           由，

           即              又.

           （II）设数列{an}的公差为d，则在中分别取k=1,2,得

    （1）

    （2）

           由（1）得

           当

           若成立

           若

              故所得数列不符合题意.

           当

           若

           若.

           综上，共有3个满足条件的无穷等差数列：

           ①{an} : an=0，即0，0，0，…；

           ②{an} : an=1，即1，1，1，…；

           ③{an} : an=2n－1，即1，3，5，…，

    （21）本小题主要考查直线、椭圆和向量等基本知识，以及推理能力和运算能力.满分12分.

           解：（I）设所求椭圆方程是

           由已知，得    所以.

           故所求的椭圆方程是

           （II）设Q（），直线

           当由定比分点坐标公式，得

          

           .

           于是   故直线l的斜率是0，.

    （22）本小题主要考查函数、不等式等基本知识，以及综合运用数学知识解决问题的能力.满分14分.

           证明：（I）任取 

           和  ②

           可知 ，

           从而 .  假设有①式知

          

           ∴不存在

           （II）由                        ③

           可知   ④

           由①式，得   ⑤

           由和②式知，   ⑥

           由⑤、⑥代入④式，得

                              

    （III）由③式可知

      （用②式）

           （用①式）


    同步练习册答案