
题目列表(包括答案和解析)
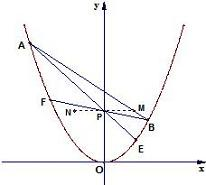 已知抛物线y=x2和三个点M(x0,y0)、P(0,y0)、N(-x0,y0)(y0≠x02,y0>0),过点M的一条直线交抛物线于A、B两点,AP、BP的延长线分别交曲线C于E、F.
已知抛物线y=x2和三个点M(x0,y0)、P(0,y0)、N(-x0,y0)(y0≠x02,y0>0),过点M的一条直线交抛物线于A、B两点,AP、BP的延长线分别交曲线C于E、F.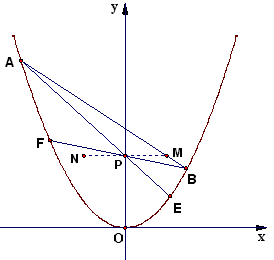
 如图,设P0是抛物线y=x2上一点,且在第一象限.过点P0作抛物线的切线,交x轴于Q1点,过Q1点作x轴的垂线,交抛物线于P1点,此时就称P0确定了P1.依此类推,可由P1确定P2,….记Pn(xn,yn),n=0,1,2,….给出下列三个结论:
如图,设P0是抛物线y=x2上一点,且在第一象限.过点P0作抛物线的切线,交x轴于Q1点,过Q1点作x轴的垂线,交抛物线于P1点,此时就称P0确定了P1.依此类推,可由P1确定P2,….记Pn(xn,yn),n=0,1,2,….给出下列三个结论: 如图,设P0是抛物线y=x2上一点,且在第一象限.过点P0作抛物线的切线,交x轴于Q1点,过Q1点作x轴的垂线,交抛物线于P1点,此时就称P0确定了P1.依此类推,可由P1确定P2,….记Pn(xn,yn),n=0,1,2,….给出下列三个结论:
如图,设P0是抛物线y=x2上一点,且在第一象限.过点P0作抛物线的切线,交x轴于Q1点,过Q1点作x轴的垂线,交抛物线于P1点,此时就称P0确定了P1.依此类推,可由P1确定P2,….记Pn(xn,yn),n=0,1,2,….给出下列三个结论:| 1 | 4 |
 某中学,由于不断深化教育改革,办学质量逐年提高.2006年至2009年高考考入一流大学人数如下:
某中学,由于不断深化教育改革,办学质量逐年提高.2006年至2009年高考考入一流大学人数如下:| 年 份 | 2006 | 2007 | 2008 | 2009 |
| 高考上线人数 | 116 | 172 | 220 | 260 |
| 年 份 | 2006 | 2007 | 2008 | 2009 |
| 年份代码x | 1 | 2 | 3 | 4 |
| 实际上线人数 | 116 | 172 | 220 | 260 |
| 模拟上线人数 | y1=a+b | y2=2a+b | y3=3a+b | y4=4a+b |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com